Tag: sampling

Simulating an inhomogeneous Poisson point process

In previous posts I described how to simulate homogeneous Poisson point processes on a rectangle, disk and triangle. But here I will simulate an inhomogeneous or nonhomogeneous Poisson point process. (Both of these terms are used, where the latter is probably more popular, but I prefer the former.) For such a point process, the points are not uniformly located on the underlying mathematical space on which the Poisson process is defined. This means that certain regions will, on average, tend to have more (or less) points than other regions of the underlying space.

Basics

Any Poisson point process is defined with a non-negative measure called the intensity or mean measure. I make the standard assumption that the intensity measure \(\Lambda\) has a derivative \(\lambda(x,y)\). (I usually write a single \(x\) to denote a point on the plane, that is \(x\in \mathbb{R}^2\), but in this post I will write the \(x\) and \(y\) and coordinates separately.) The function \(\lambda(x,y)\) is often called the intensity function or just intensity, which I further assume is bounded, so \(\lambda(x,y)<\infty\) for all points in a simulation window \(W\). Finally, I assume that the simulation window \(W\) is a rectangle, but later I describe how to lift that assumption.

Number of points

To simulate a point process, the number of points and the point locations in the simulation window \(W\) are needed. For any Poisson point process, the number of points is a Poisson random variable with a parameter (that is, a mean) \(\Lambda(W)\), which under our previous assumptions is given by the integral

$$\Lambda(W)=\int_W \lambda(x,y)dxdy. $$

Assuming we can evaluate such an integral analytically or numerically, then the number of points is clearly not difficult to simulate.

Locations of points

The difficulty lies in randomly positioning the points. But a defining property of the Poisson point process is its independence, which allows us to treat each point completely independently. Positioning each point then comes down to suitably simulating two (or more) random variables for Poisson point processes in two (or higher) dimensions. Similarly, the standard methods used for simulating continuous random variables can be applied to simulating random point locations of a Poisson point process.

In theory, you can rescale the intensity function with the total measure of the simulation window, giving

$$f(x,y):=\frac{\lambda(x,y)}{\Lambda(W)}. $$

We can then interpret this rescaled intensity function \(f(x,y)\) as the joint probability density of two random variables \(X\) and \(Y\), because it integrates to one,

$$\int_W f(x,y)dxdy=1.$$

Clearly the method for simulating an inhomogeneous Poisson point process depends on the nature of the intensity function. For the inhomogeneous case, the random variables \(X\) and \(Y\) are, in general, not independent.

Transformation

To simulate an inhomogeneous Poisson point process, one method is to first simulate a homogeneous one, and then suitably transform the points according to deterministic function. For simple random variables, this transformation method is quick and easy to implement, if we can invert the probability distribution. For example, a uniform random variable \(U\) defined on the interval \((0,1)\) can be used to give an exponential random variable by applying the transformation \(h(u)= -(1/\lambda)\log(u)\), where \(\lambda>0\), meaning \(h(U)\) is an exponential random variable with parameter \(\lambda>0\) (or mean \(1/\lambda\)).

Similarly for Poisson point processes, the transformation approach is fairly straightforward in a one-dimensional setting, but generally doesn’t work easily in two (or higher) dimensions. The reason being that often we cannot simulate the random variables \(X\) and \(Y\) independently, which means, in practice, we need first to simulate one random variable, then the other.

It is a bit easier if we can re-write the rescaled intensity function or joint probability density \(f(x,y)\) as a product of single-variable functions \(f_X(x)\) and \(f_Y(y)\), meaning the random variables \(X\) and \(Y\) are independent. We can then simulate independently the random variables \(X\) and \(Y\), corresponding to the \(x\) and \(y\) coordinates of the points. But this would still require integrating and inverting the functions.

Markov chain Monte Carlo

A now standard way to simulate jointly distributed random variables is to use Markov chain Monte Carlo (MCMC), which we can also use to simulate the the \(X\) and \(Y\) random variables. Applying MCMC methods is simply applying random point process operations repeatedly to all the points. But this is a bit too tricky and involved. Instead I’ll use a general yet simpler method based on thinning.

Thinning

The thinning method is the arguably the simplest and most general way to simulate an inhomogeneous Poisson point process. If you’re unfamiliar with thinning, I recommend my previous post on thinning and the material I cite.

This simulation method is simply a type of acceptance-rejection method for simulating random variables. More specifically, it is the acceptance-rejection or rejection method, attributed to the great John von Neumann, for simulating a continuous random variable, say \(X\), with some known probability density \(f(x)\). The method accepts/retains or rejects/thins the outcome of each random variable/point depending on the outcome of a uniform random variable associated with each random variable/point.

The thinning or acceptance-rejection method is also appealing because it is an example of a perfect simulation method, which means the distribution of the simulated random variables or points will not be an approximation. This can be contrasted with typical MCMC methods, which, in theory, reach the desired distribution of the random variables in infinite time, which is clearly not possible in practice.

Simulating the homogeneous Poisson point process

First simulate a homogeneous Poisson point process with intensity value \(\lambda^*\), which is an upper bound of the intensity function \(\lambda(x,y)\). The simulation step is the easy part, but what value is \(\lambda^*\)?

I will use the maximum value that the intensity function \(\lambda(x,y)\) takes, which I denote by

$$ \lambda_{\max}:=\max_{(x,y)\in W}\lambda(x,y),$$

so I set \(\lambda^*=\lambda_{\max}\). Of course with \(\lambda^*\) being an upper bound, you can use any larger \(\lambda\)-value, so \(\lambda^*\geq \lambda_{\max}\), but that just means more points will need to be thinned.

Scientific programming languages have implemented algorithms that find or estimate minima of mathematical functions, meaning such an algorithm just needs to find the \((x,y)\) point that gives the minimum value of \(-\lambda(x,y)\), which corresponds to the maximum value of \(\lambda(x,y)\). What is very important is that the minimization procedure can handle constraints on the \(x\) and \(y\) values, which in our case of a rectangular simulation window \(W\) are sometimes called box constraints.

Thinning the Poisson point process

All we need to do now is to thin the homogeneous Poisson point process with the thinning probability function

$$1-p(x,y)=\frac{\lambda(x,y)}{\lambda^*}.$$

This will randomly remove the points so the remaining points will form a inhomogeneous Poisson point process with intensity function
$$ (1-p(x,y))\lambda^* =\lambda(x,y).$$
As a result, we can see that provided \(\lambda^*\geq \lambda_{\max}>0\), this procedure will give the right intensity function \(\lambda(x,y)\). I’ll skip the details on the point process still being Poisson after thinning, as I have already covered this in the thinning post.

Empirical check

You can run an empirical check by simulating the point process a large number (say \(10^3\) or \(10^4\)) of times, and collect statistics on the number of points. As the number of simulations increases, the average number of points should converge to the intensity measure \(\Lambda(W)\), which is given by (perhaps numerically) evaluating the integral

$$\Lambda(W)=\int_W \lambda(x,y)dxdy.$$

This is a test for the intensity measure, a type of first moment, which will work for the intensity measure of any point process. But for Poisson point processes, the variance of the number of points will also converge to intensity measure \(\Lambda(W)\), giving a second empirical test based on second moments.

An even more thorough test would be estimating an empirical distribution (that is, performing and normalizing a histogram) on the number of points. These checks will validate the number of points, but not the positioning of the points. In my next post I’ll cover how to perform these tests.

Results

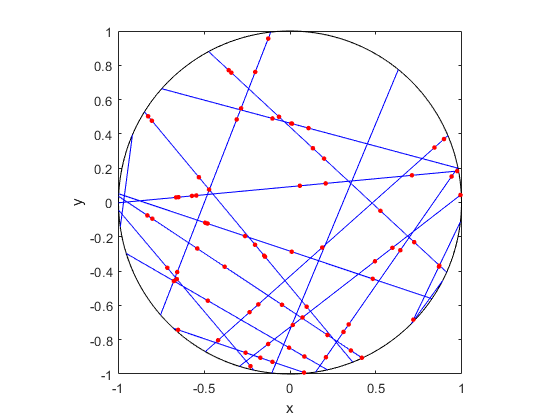
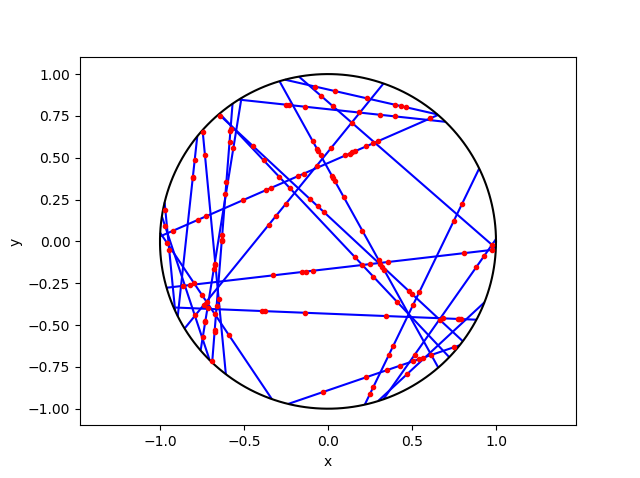
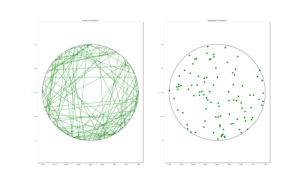
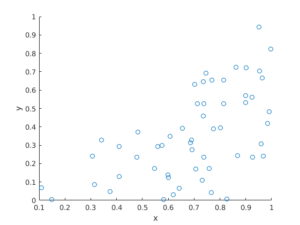
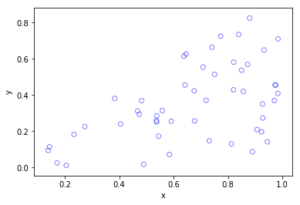
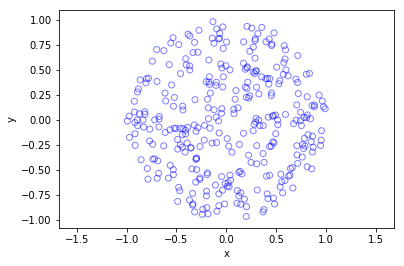
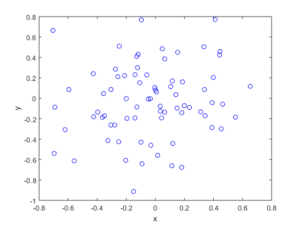
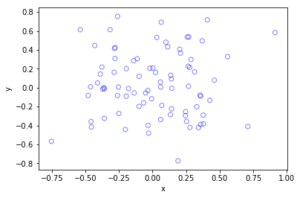
The homogeneous Poisson point process with intensity function \(\lambda(x)=100\exp(-(x^2+y^2)/s^2)\), where \(s=0.5\). The results look similar to those in the thinning post, where the thinned points (that is, red circles) are generated from the same Poisson point process as the one that I have presented here.

MATLAB

Python

Method extensions

We can extend the thinning method for simulating inhomogeneous Poisson point processes a couple different ways.

Using an inhomogeneous Poisson point process

The thinning method does not need to be applied to a homogeneous Poisson point process with intensity \(\lambda^*\). In theory, we could have simulated a suitably inhomogeneous Poisson point process with intensity function \(\lambda^*(x,y)\), which has the condition

$$ \lambda^*(x,y)\geq \lambda(x,y), \quad \forall (x,y)\in W .$$

Then this Poisson point process is thinned. But then we would still need to simulate the underlying Poisson point process, which often would be as difficult to simulate.

Partitioning the simulation window

Perhaps the intensity of the Poisson point process only takes two values, \(\lambda_1\) and \(\lambda_2\), and the simulation window \(W\) can be nicely divided or partitioned into two disjoints sets \(B_1\) and \(B_2\) (that is, \(B_1\cap B_2=\emptyset\) and \(B_1\cup B_2=W\)), corresponding to the subregions of the two different intensity values. The Poisson independence property allows us to simulate two independent Poisson point processes on the two subregions.

This approach only works for a piecewise constant intensity function. But if if the intensity function \(\lambda(x)\) varies wildly, the simulation window can be partitioned into subregions \(B_1\dots,B_m\) for different ranges of the intensity function \(\lambda(x)\). This allows us to simulate independent homogeneous Poisson point processes with different densities \(\lambda^*_1\dots, \lambda^*_m\), where for each subregion \(B_i\) we set

$$ \lambda^*_i:=\max_{x\in B_i}\lambda(x,y).$$

The resulting Poisson point processes are then suitably thinned, resulting in a more efficient simulation method. (Although I imagine the gain would often be small.)

Non-rectangular simulation windows

If you want to simulate on non-rectangular regions, which is not a disk or triangle, then the easiest way is to simulate a Poisson point process on a rectangle \(R\) that completely covers the simulation window, so \(W \subset R\subset \mathbb{R}^2\), and then set the intensity function \(\lambda \) to zero for the region outside the simulation window \(W\), that is \(\lambda (x,y)=0\) when \((x,y)\in R\setminus W\).

Further reading

In Section 2.5.2 of Stochastic Geometry and its Applications by Chiu, Stoyan, Kendall and Mecke, there is an outline of the thinning method that I used. The same simulation section appears in the previous edition by Kendall and Mecke, though these books in general have little material on simulation methods.

More details on the thinning method and its connection to acceptance-rejection sampling are given in Section 2.3 of the applications-oriented book Poisson Point Processes by Streit. The acceptance-rejection method is covered in, for example, books on Monte Carlo methods, including Monte Carlo Strategies in Scientific Computing by Liu (in Section 2.2 )and Monte Carlo Methods in Financial Engineering by Glasserman (in Section 2.2.2). This method and others for simulating generals random variable are covered in stochastic simulation books such as Uniform Random Variate Generation by Devroye and Stochastic Simulation: Algorithms and Analysis by Asmussen and Glynn.

Kroese and Botev have a good introduction to stochastic simulation in the edited collection Stochastic Geometry, Spatial Statistics and Random Fields : Models and Algorithms by Schmidt, where the relevant chapter (number 12) is also freely available online. And of course there are lectures notes on the internet that cover simulation material.

Code

All code from my posts, as always, can be found on the my GitHub repository. The code for this post is located here. You can see that the code is very similar to that of the thinning code, which served as the foundation for this code. (Note how we now keep the points, so in the code the > has become < on the line where the uniform variables are generated).

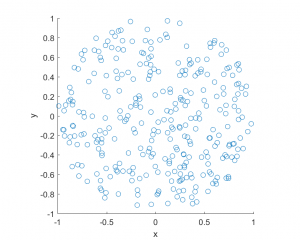
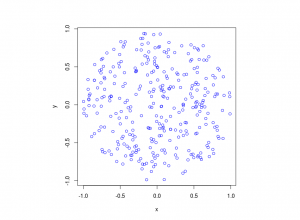
I have implemented the code in MATLAB and Python with an intensity function \(\lambda(x,y)=100\exp(-(x^2+y^2)/s^2)\), where \(s>0\) is a scale parameter. Note that in the minimization step, the box constraints are expressed differently in MATLAB and Python: MATLAB first takes the minimum values then the maximum values, whereas Python first takes the \(x\)-values then the \(y\)-values.

The code presented here does not have the empirical check, which I described above, but it is implemented in the code located here. For the parameters used in the code, the total measure is \(\Lambda(W)\approx 77.8068\), meaning each simulation will generate on average almost seventy-eight points.

I have stopped writing code in R for a couple of reasons, but mostly because anything I could think of simulating in R can already be done in the spatial statistics library spatstat. I recommend the book Spatial Point Patterns, co-authored by the spatstat’s main contributor, Adrian Baddeley.

MATLAB

I have used the fmincon function to find the point that gives the minimum of \(-\lambda(x,y)\).

%Simulation window parameters
xMin=-1;xMax=1;
yMin=-1;yMax=1;
xDelta=xMax-xMin;yDelta=yMax-yMin; %rectangle dimensions
areaTotal=xDelta*yDelta; %area of rectangle

s=0.5; %scale parameter

%Point process parameters
fun_lambda=@(x,y)(100*exp(-((x).^2+(y).^2)/s^2));%intensity function

%%%START -- find maximum lambda -- START %%%
%For an intensity function lambda, given by function fun_lambda,
%finds the maximum of lambda in a rectangular region given by
%[xMin,xMax,yMin,yMax].
funNeg=@(x)(-fun_lambda(x(1),x(2))); %negative of lambda
%initial value(ie centre)
xy0=[(xMin+xMax)/2,(yMin+yMax)/2];%initial value(ie centre)
%Set up optimization step
options=optimoptions('fmincon','Display','off');
%Find largest lambda value
[~,lambdaNegMin]=fmincon(funNeg,xy0,[],[],[],[],...
[xMin,yMin],[xMax,yMax],'',options);
lambdaMax=-lambdaNegMin;
%%%END -- find maximum lambda -- END%%%

%define thinning probability function
fun_p=@(x,y)(fun_lambda(x,y)/lambdaMax);

%Simulate Poisson point process
numbPoints=poissrnd(areaTotal*lambdaMax);%Poisson number of points
xx=xDelta*(rand(numbPoints,1))+xMin;%x coordinates of Poisson points
yy=xDelta*(rand(numbPoints,1))+yMin;%y coordinates of Poisson points

%calculate spatially-dependent thinning probabilities
p=fun_p(xx,yy);

%Generate Bernoulli variables (ie coin flips) for thinning
booleRetained=rand(numbPoints,1)<p; %points to be thinned

%x/y locations of retained points
xxRetained=xx(booleRetained); yyRetained=yy(booleRetained);

%Plotting
plot(xxRetained,yyRetained,'bo'); %plot retained points
xlabel('x');ylabel('y');

The box constraints for the optimization step were expressed as:

[xMin,yMin],[xMax,yMax]
Python

I have used the minimize function in SciPy.

import numpy as np; #NumPy package for arrays, random number generation, etc
import matplotlib.pyplot as plt #For plotting
from scipy.optimize import minimize #For optimizing
from scipy import integrate

#Simulation window parameters
xMin=-1;xMax=1;
yMin=-1;yMax=1;
xDelta=xMax-xMin;yDelta=yMax-yMin; #rectangle dimensions
areaTotal=xDelta*yDelta;

s=0.5; #scale parameter

#Point process parameters
def fun_lambda(x,y):
return 100*np.exp(-(x**2+y**2)/s**2); #intensity function

###START -- find maximum lambda -- START ###
#For an intensity function lambda, given by function fun_lambda,
#finds the maximum of lambda in a rectangular region given by
#[xMin,xMax,yMin,yMax].
def fun_Neg(x):
return -fun_lambda(x[0],x[1]); #negative of lambda

xy0=[(xMin+xMax)/2,(yMin+yMax)/2];#initial value(ie centre)
#Find largest lambda value
resultsOpt=minimize(fun_Neg,xy0,bounds=((xMin, xMax), (yMin, yMax)));
lambdaNegMin=resultsOpt.fun; #retrieve minimum value found by minimize
lambdaMax=-lambdaNegMin;
###END -- find maximum lambda -- END ###

#define thinning probability function
def fun_p(x,y):
return fun_lambda(x,y)/lambdaMax;

#Simulate a Poisson point process
numbPoints = np.random.poisson(lambdaMax*areaTotal);#Poisson number of points
xx = np.random.uniform(0,xDelta,((numbPoints,1)))+xMin;#x coordinates of Poisson points
yy = np.random.uniform(0,yDelta,((numbPoints,1)))+yMin;#y coordinates of Poisson points

#calculate spatially-dependent thinning probabilities
p=fun_p(xx,yy);

#Generate Bernoulli variables (ie coin flips) for thinning
booleRetained=np.random.uniform(0,1,((numbPoints,1)))<p; #points to be thinned

#x/y locations of retained points
xxRetained=xx[booleRetained]; yyRetained=yy[booleRetained];

#Plotting
plt.scatter(xxRetained,yyRetained, edgecolor='b', facecolor='none', alpha=0.5 );
plt.xlabel("x"); plt.ylabel("y");
plt.show();

The box constraints were expressed as:

(xMin, xMax), (yMin, yMax)
Julia

After writing this post, I later wrote the code in Julia. The code is here and my thoughts about Julia are here.

Simulating a Poisson point process on a triangle

The title gives it away. But yes, after  two posts about simulating a Poisson point process  on a rectangle and disk, the next shape is a triangle. Useful, right?

Well, I actually had to do this once for a part of something larger. You can divide  polygons, regular or irregular, into triangles, which is often called triangulation, and there is much code that does triangulation.  Using the independence property of the Poisson process, you can then simulate a Poisson point process on each triangle, and you end up with a Poisson point process on a polygon.

But the first step is to do it on a triangle. Consider a general triangle with its three corners labelled \(\textbf{A}\), \(\textbf{B}\) and \(\textbf{C}\). Again, simulating a Poisson point process comes down to the number of points and the locations of points.

Method

Number of points

The number of points of a homogeneous Poisson point process  in any shape with with area \(A\) is simply a Poisson random variable with mean  \(\lambda A\), where \(A\) is the area of the shape. For the triangle’s area, we just uses Herron’s formula, which says that a triangle with sides \(a\), \(b\), and \(c\)  has the area \(A=\sqrt{s(s-a)(s-b)(s-c)}\), where \(s=(a+b+c)/2\), which means you just need to use Pythagoras’ theorem for  the lengths \(a\), \(b\), and \(c\). Interestingly, this standard formula can be prone to numerical error if the triangle is very thin or needle-shaped. A more secure and stable expression is

\(A=\frac{1}{4}\sqrt{ (a+(b+c)) (c-(a-b)) (c+(a-b)) (a+(b-c)) },\)

where the brackets do matter; see Section 2.5 in the book by Higham.

Of course in MATLAB you can just use the function polyarea or the function with the same name in R.

Now just generate or simulate Poisson random variables with mean (or parameter)  \(\lambda A\). In MATLAB,  use the poissrnd function with the argument \(\lambda A\). In R, it is done similarly with the standard  function rpois . In Python, we can use either the scipy.stats.poisson or numpy.random.poisson function from the SciPy or NumPy libraries.

Locations of points

We need to position all the points randomly and uniformly on a triangle.  As with the previous two simulation cases, to position a single point \((x, y)\), you first need to produce two random uniform variables on the unit interval \((0,1)\), say \(U\) and \(V\). I’ll denote the \(x\) and \(y\) coordinates of point by \(x_{\textbf{A}}\) and \(y_{\textbf{A}}\), and similarly for the other two points.  To get the random \(x\) and \(y\) values, you use these two formulas:

\(x=\sqrt{U} x_{\textbf{A}}+\sqrt{U}(1-V x_{\textbf{B}})+\sqrt{U}V x_{\textbf{C}}\)

\(y=\sqrt{U} y_{\textbf{A}}+\sqrt{U}(1-V y_{\textbf{B}})+\sqrt{U}V y_{\textbf{C}}\)

Done. A Poisson point process simulated on a triangle .

Code

I now present some code in MATLAB, R and Python, which you can see are all very similar.  To avoid using a for-loop and employing instead MATLAB’s inbuilt vectorization, I use the dot notation for the product \(\sqrt{U}V\). In R and Python (using SciPy), that’s done automatically.

MATLAB


%Simulation window parameters -- points A,B,C of a triangle
xA=0;xB=1;xC=1; %x values of three points
yA=0;yB=0;yC=1; %y values of three points

%Point process parameters
lambda=100; %intensity (ie mean density) of the Poisson process

%calculate sides of trinagle
a=sqrt((xA-xB)^2+(yA-yB)^2);
b=sqrt((xB-xC)^2+(yB-yC)^2);
c=sqrt((xC-xA)^2+(yC-yA)^2);
s=(a+b+c)/2; %calculate semi-perimeter

%Use Herron's forumula -- or use polyarea
areaTotal=sqrt(s*(s-a)*(s-b)*(s-c)); %area of triangle

%Simulate Poisson point process
numbPoints=poissrnd(areaTotal*lambda);%Poisson number of points
U=(rand(numbPoints,1));%uniform random variables
V=(rand(numbPoints,1));%uniform random variables

xx=sqrt(U)*xA+sqrt(U).*(1-V)*xB+sqrt(U).*V*xC;%x coordinates of points
yy=sqrt(U)*yA+sqrt(U).*(1-V)*yB+sqrt(U).*V*yC;%y coordinates of points

%Plotting
scatter(xx,yy);
xlabel('x');ylabel('y');

R

Note: it is a bit tricky to write “<-” in the R code (as it automatically changes to the html equivalent in the HTML editor I am using), so I have usually used “=” instead of the usual “<-”.


#Simulation window parameters -- points A,B,C of a triangle
xA=0;xB=1;xC=1; #x values of three points
yA=0;yB=0;yC=1; #y values of three points

#Point process parameters
lambda=100; #intensity (ie mean density) of the Poisson process

#calculate sides of trinagle
a=sqrt((xA-xB)^2+(yA-yB)^2);
b=sqrt((xB-xC)^2+(yB-yC)^2);
c=sqrt((xC-xA)^2+(yC-yA)^2);
s=(a+b+c)/2; #calculate semi-perimeter

#Use Herron's forumula to calculate area
areaTotal=sqrt(s*(s-a)*(s-b)*(s-c)); #area of triangle

#Simulate a Poisson point process
numbPoints=rpois(1,areaTotal*lambda);#Poisson number of points
U=runif(numbPoints);#uniform random variables
V=runif(numbPoints);#uniform random variables

xx=sqrt(U)*xA+sqrt(U)*(1-V)*xB+sqrt(U)*V*xC;#x coordinates of points
yy=sqrt(U)*yA+sqrt(U)*(1-V)*yB+sqrt(U)*V*yC;#y coordinates of points

#Plotting
plot(xx,yy,'p',xlab='x',ylab='y',col='blue');

Simulating a Poisson point process in R is even easier, with the amazing spatial statistics library spatstat. You just need to define the triangular window.

#Simulation window parameters -- points A,B,C of a triangle
xA=0;xB=1;xC=1; #x values of three points
yA=0;yB=0;yC=1; #y values of three points

#Point process parameters
lambda=100; #intensity (ie mean density) of the Poisson process

library("spatstat");
#create triangle window object
windowTriangle=owin(poly=list(x=c(xA,xB,xC), y=c(yA,yB,yC)));
#create Poisson "point pattern" object
ppPoisson=rpoispp(lambda,win=windowTriangle)
plot(ppPoisson); #Plot point pattern object
#retrieve x/y values from point pattern object
xx=ppPoisson$x;
yy=ppPoisson$y;

Python

Note: “lambda” is a reserved word in Python (and other languages), so I have used “lambda0” instead.

#import libraries
import numpy as np
import scipy.stats
import matplotlib.pyplot as plt

#Simulation window parameters -- points A,B,C of a triangle
xA=0;xB=1;xC=1; #x values of three points
yA=0;yB=0;yC=1; #y values of three points

#Point process parameters
lambda0=100; #intensity (ie mean density) of the Poisson process

#calculate sides of trinagle
a=np.sqrt((xA-xB)**2+(yA-yB)**2);
b=np.sqrt((xB-xC)**2+(yB-yC)**2);
c=np.sqrt((xC-xA)**2+(yC-yA)**2);
s=(a+b+c)/2; #calculate semi-perimeter

#Use Herron's forumula to calculate area -- or use polyarea
areaTotal=np.sqrt(s*(s-a)*(s-b)*(s-c)); #area of triangle

#Simulate a Poisson point process
numbPoints = scipy.stats.poisson(lambda0*areaTotal).rvs();#Poisson number of points
U = scipy.stats.uniform.rvs(0,1,((numbPoints,1)));#uniform random variables
V= scipy.stats.uniform.rvs(0,1,((numbPoints,1)));#uniform random variables

xx=np.sqrt(U)*xA+np.sqrt(U)*(1-V)*xB+np.sqrt(U)*V*xC;#x coordinates of points
yy=np.sqrt(U)*yA+np.sqrt(U)*(1-V)*yB+np.sqrt(U)*V*yC;#y coordinates of points

#Plotting
plt.scatter(xx,yy, edgecolor='b', facecolor='none', alpha=0.5 );
plt.xlabel("x"); plt.ylabel("y");

Results

MATLAB

R

Python

Further reading

The topic of placing a single point uniformly on a general triangle is discussed in this StackExchange post.  For the formulas, it cites the paper “Shape distributions” by Osada, Funkhouser, Chazelle and Dobkin”, where no proof is given.

I originally looked at placing single points in cells of a Dirichlet or Voronoi tesselation — terms vary. There is a lot of literature on this topic, particularly when the seeds of the cells form a Poisson point process. The references in the articles on Wikipedia and MathWorld are good starting points.

Correction

In a previous version of this blog, there was an error in the two Cartesian formula for randomly simulating a point in a triangle. This has been fixed, but the error never existed in the code.

Simulating a Poisson point process on a disk

Sometimes one needs to simulate a Poisson point process on a disk. I know I often do. A disk or disc, depending on your spelling preference, is isotropic or rotationally-invariant, so a lot of my simulations of a Poisson point process happen in a circular simulation window when I am considering such a setting. For example, maybe you want to consider a single wireless receiver in a Poisson network of wireless transmitters, which only cares about the distance to a transmitter. Alternatively, maybe you want to randomly sprinkle a virtual cake. What to do? A Poisson point process on a disk is the answer.

In this post I will simulate a Poisson point process with intensity \(\lambda>0\) on a disk with radius \(r>0\).

Steps

The simulation steps are very similar to those in the previous post where I simulated a  homogeneous Poisson point process on a rectangle, and I suggest going back to that post if you are not familiar with the material. The main difference between simulation on a rectangle and a disk is the positioning of the points, but first we’ll look at the number of points.

Number of points

The number of points of a Poisson point process falling within a circle of radius \(r>0\) is a Poisson random variable with mean  \(\lambda A\), where \(A=\pi r^2\) is the area of the disk. As in the rectangular case, this is the most complicated part of the simulation procedure. But as long as your preferred programming language can produce (pseudo-)random numbers according to a Poisson distribution, you can simulate a homogeneous Poisson point process on a disk.

To do this in MATLAB,  use the poissrnd function with the argument \(\lambda A\). In R, it is done similarly with the standard  function rpois . In Python, we can use either the scipy.stats.poisson or numpy.random.poisson function from the SciPy or NumPy libraries.

Locations of points

We need to position all the points randomly and uniformly on a disk. In the case of the rectangle, we worked in Cartesian coordinates. It is then natural that we now work in polar coordinates.  I’ll denote the angular and radial coordinate respectively by \(\theta\) and \(\rho\). To generate the random angular (or \(\theta\)) values, we simply produce uniform random variables between zero and one, which is what all standard (pseudo-)random number generators do in programming languages. But we then multiply all these numbers by \(2\pi\), meaning that all the numbers now fall between \(0\) and \(2\pi\).

To generate the random radial (or \(\rho\)) values, a reasonable guess would be to do the same as before and generate uniform random variables between zero and one, and then multiply them by the disk radius \(r\). But that would be wrong.

Before multiplying uniform random variables by the radius, we must take the square root of all the random numbers. We then multiply them by the radius, generating random variables between \(0\) and \(r\). (We must take the square root because the area element of a sector or disk is proportional to the radius squared, and not the radius.) These random numbers do not have a uniform distribution, due to the square root, but in fact their distribution is an example of the triangular distribution, which is defined with three real-valued parameters \(a\), \(b\) and \(c\), and for our case, set \(a=0\) and \(b=c=r\).

In summary, if \(U\) and \(V\) are two independent uniform random variables on \((0,1)\), then random point located uniformly on a disk of radius \(r\) has the polar coordinates \((r\sqrt(U), 2\pi V)\).

From polar to Cartesian coordinates

That’s it. We have generated polar coordinates for points randomly and uniformly located in a disk. But to plot the points, often we have to convert coordinates back to Cartesian form. This is easily done in MATLAB with the pol2cart function. In languages without such a function, trigonometry comes to the rescue: \(x=\rho\cos(\theta)\) and \(y=\rho\sin(\theta)\).

Equal x and y axes

Sometimes the plotted points more resemble points on an ellipse than a disk due to the different scaling of the x and y axes. To fix this in MATLAB, run the command: axis square. In Python, set axis(‘equal’) in your plot; see this page for a demonstration.

Code

I’ll now give some code in MATLAB, R and Python, which, as you can see, are all very similar

MATLAB
%Simulation window parameters
r=1; %radius of disk
xx0=0; yy0=0; %centre of disk

areaTotal=pi*r^2; %area of disk
 
%Point process parameters
lambda=100; %intensity (ie mean density) of the Poisson process
 
%Simulate Poisson point process
numbPoints=poissrnd(areaTotal*lambda);%Poisson number of points
theta=2*pi*(rand(numbPoints,1)); %angular coordinates
rho=r*sqrt(rand(numbPoints,1)); %radial coordinates

%Convert from polar to Cartesian coordinates
[xx,yy]=pol2cart(theta,rho); %x/y coordinates of Poisson points

%Shift centre of disk to (xx0,yy0)
xx=xx+xx0;
yy=yy+yy0;
 
%Plotting
scatter(xx,yy);
xlabel('x');ylabel('y');
axis square;
R

Note: it is a bit tricky to write “<-” in the R code (as it automatically changes to the html equivalent in the HTML editor I am using), so I have usually used “=” instead of the usual “<-”.

#Simulation window parameters
r=1; #radius of disk
xx0=0; yy0=0; #centre of disk

areaTotal=pi*r^2; #area of disk

#Point process parameters
lambda=100; #intensity (ie mean density) of the Poisson process

#Simulate Poisson point process
numbPoints=rpois(1,areaTotal*lambda);#Poisson number of points
theta=2*pi*runif(numbPoints);#angular  of Poisson points
rho=r*sqrt(runif(numbPoints));#radial coordinates of Poisson points

#Convert from polar to Cartesian coordinates
xx=rho*cos(theta);
yy=rho*sin(theta);

#Shift centre of disk to (xx0,yy0)
xx=xx+xx0;
yy=yy+yy0;

#Plotting
par(pty="s")
plot(xx,yy,'p',xlab='x',ylab='y',col='blue');

Of course, with the amazing spatial statistics library spatstat, simulating a Poisson point process in R is even easier.

library("spatstat"); #load spatial statistics library
#create Poisson "point pattern" object
ppPoisson=rpoispp(lambda,win=disc(radius=r,centre=c(xx0,yy0))) 
plot(ppPoisson); #Plot point pattern object
#retrieve x/y values from point pattern object
xx=ppPoisson$x; 
yy=ppPoisson$y;

Actually, you can even do it all in two lines: one for loading the spatstat library and one for creating and plotting the point pattern object.

Python

Note: “lambda” is a reserved word in Python (and other languages), so I have used “lambda0” instead.

import numpy as np; #NumPy package for arrays, random number generation, etc
import matplotlib.pyplot as plt #for plotting

#Simulation window parameters
r=1;  #radius of disk
xx0=0; yy0=0; #centre of disk
areaTotal=np.pi*r**2; #area of disk

#Point process parameters
lambda0=100; #intensity (ie mean density) of the Poisson process

#Simulate Poisson point process
numbPoints = np.random.poisson(lambda0*areaTotal);#Poisson number of points
theta=2*np.pi*np.random.uniform(0,1,numbPoints); #angular coordinates 
rho=r*np.sqrt(np.random.uniform(0,1,numbPoints)); #radial coordinates 

#Convert from polar to Cartesian coordinates
xx = rho * np.cos(theta);
yy = rho * np.sin(theta);

#Shift centre of disk to (xx0,yy0) 
xx=xx+xx0; yy=yy+yy0;

#Plotting
plt.scatter(xx,yy, edgecolor='b', facecolor='none', alpha=0.5 );
plt.xlabel("x"); plt.ylabel("y");
plt.axis('equal');
Julia

After writing this post, I later wrote the code in Julia. The code is here and my thoughts about Julia are here.

Results

MATLAB
R 
Python  

Further reading

The third edition of the classic book Stochastic Geometry and its Applications by Chiu, Stoyan, Kendall and Mecke details on page 54 how to uniformly place points on a disk, which they call the radial way. The same simulation section appears in the previous edition by Stoyan, Kendall and Mecke (Chiu didn’t appear as an author until the current edition), though these books in general have little material on simulation methods. There is the book Spatial Point Patterns: Methodology and Applications with R written by spatial statistics experts  Baddeley, Rubak and Turner, which covers the spatial statistics (and point process simulation) R-package spatstat.

Simulating a homogeneous Poisson point process on a rectangle

This is the first of a series of posts about simulating Poisson point processes. I’ll start with arguably the simplest Poisson point process on two-dimensional space, which is the homogeneous one defined on a rectangle. Let’s say that we we want to simulate a Poisson point process with intensity \(\lambda>0\) on a (bounded) rectangular region, for example, the rectangle \([0,w]\times[0,h]\) with dimensions \(w>0\) and \(h>0\) and area \(A=wh\). We assume for now that the bottom left corner of the rectangle is at the origin.

Steps

Number of points

The number of points in the rectangle  \([0,w]\times[0,h]\) is a Poisson random variable with mean \(\lambda A\). In other words, this random variable is distributed according to the Poisson distribution with parameter \(\lambda A\), and not just \(\lambda\), because the number of points depends on the size of the simulation region.

This is the most complicated part of the simulation procedure. As long as your preferred programming language can produce (pseudo-)random numbers according to a Poisson distribution, you can simulate a homogeneous Poisson point process. There’s a couple of different ways used to simulate Poisson random variables, but we will skip the details. In MATLAB, it is done by using the poissrnd function with the argument \(\lambda A\). In R, it is done similarly with the standard  function rpois . In Python, we can use either the scipy.stats.poisson or numpy.random.poisson function from the SciPy or NumPy libraries.

Location of points

The points now need to be positioned randomly, which is done by using Cartesian coordinates. For a homogeneous Poisson point process, the \(x\) and \(y\) coordinates of each point are independent uniform points, which is also the case for the binomial point process, covered in a previous post. For the rectangle \([0,w]\times[0,h]\), the \(x\) coordinates are uniformly sampled on the interval \([0,w]\), and similarly for the \(y\) coordinates. If the bottom left corner of rectangle is located at the point \((x_0,y_0)\), then we just have to shift the random \(x\) and \(y\) coordinates by respectively adding \(x_0\) and \(y_0\).

Every scientific programming language has a random uniform number generator because it is the default random number generator. In MATLAB, R and SciPy, it is respectively rand, runif and scipy.stats.uniform.

Code

Here is some code that I wrote for simulating a homogeneous Poisson point process on a rectangle. You will notice that in all the code samples the part that simulates the Poisson point process requires only three lines of code: one line for the number of points and two lines lines for the \(x\) and \(y\) coordinates  of the points.

MATLAB
%Simulation window parameters
xMin=0;xMax=1;
yMin=0;yMax=1;
xDelta=xMax-xMin;yDelta=yMax-yMin; %rectangle dimensions
areaTotal=xDelta*yDelta;

%Point process parameters
lambda=100; %intensity (ie mean density) of the Poisson process

%Simulate Poisson point process
numbPoints=poissrnd(areaTotal*lambda);%Poisson number of points
xx=xDelta*(rand(numbPoints,1))+xMin;%x coordinates of Poisson points
yy=yDelta*(rand(numbPoints,1))+yMin;%y coordinates of Poisson points

%Plotting
scatter(xx,yy);
xlabel('x');ylabel('y');
R

Note: it is a bit tricky to write “<-” in the R code (as it automatically changes to the html equivalent in the HTML editor I am using), so I have usually used “=” instead of the usual “<-”.

#Simulation window parameters
xMin=0;xMax=1;
yMin=0;yMax=1;
xDelta=xMax-xMin;yDelta=yMax-yMin; #rectangle dimensions
areaTotal=xDelta*yDelta;

#Point process parameters
lambda=100; #intensity (ie mean density) of the Poisson process

#Simulate Poisson point process
numbPoints=rpois(1,areaTotal*lambda);#Poisson number of points
xx=xDelta*runif(numbPoints)+xMin;#x coordinates of Poisson points
yy=yDelta*runif(numbPoints)+yMin;#y coordinates of Poisson points

#Plotting
plot(xx,yy,'p',xlab='x',ylab='y',col='blue');
Python

Note: “lambda” is a reserved word in Python (and other languages), so I have used “lambda0” instead.

import numpy as np
import scipy.stats
import matplotlib.pyplot as plt

#Simulation window parameters
xMin=0;xMax=1;
yMin=0;yMax=1;
xDelta=xMax-xMin;yDelta=yMax-yMin; #rectangle dimensions
areaTotal=xDelta*yDelta;

#Point process parameters
lambda0=100; #intensity (ie mean density) of the Poisson process

#Simulate Poisson point process
numbPoints = scipy.stats.poisson( lambda0*areaTotal ).rvs()#Poisson number of points
xx = xDelta*scipy.stats.uniform.rvs(0,1,((numbPoints,1)))+xMin#x coordinates of Poisson points
yy = yDelta*scipy.stats.uniform.rvs(0,1,((numbPoints,1)))+yMin#y coordinates of Poisson points
#Plotting
plt.scatter(xx,yy, edgecolor='b', facecolor='none', alpha=0.5 )
plt.xlabel("x"); plt.ylabel("y")
Julia

After writing this post, I later wrote the code in Julia. The code is here and my thoughts about Julia are here.

Results

MATLAB

PoissonMatlab

R

PoissonR

Python

PoissonPython

Higher dimensions

If you want to simulate a Poisson point process in a three-dimensional box (typically called a cuboid or rectangular prism), you just need two modifications.

For a box \([0,w]\times[0,h]\times[0,\ell]\), the number of points now a Poisson random variable with mean \(\lambda V\), where \(V= wh\ell\) is the volume of the box. (For higher dimensions, you need to use $n$-dimensional volume.)

To position the points in the box, you just need an additional uniform variable for the extra coordinate. In other words, the \(x\), \(y\) and \(z\) coordinates are uniformly and independently sampled on the respective intervals \([0,w]\), \([0,h]\), \([0,\ell]\). The more dimensions, the more uniform random variables.

And that’s it.

Further reading

For simulation of point processes, see, for example, the books Statistical Inference and Simulation for Spatial Point Processes by Møller and Waagepetersen, or Stochastic Geometry and its Applications by Chiu, Stoyan, Kendall and Mecke.

There are books written by spatial statistics experts such as Stochastic Simulation by Ripley and Spatial Point Patterns: Methodology and Applications with R by Baddeley, Rubak and Turner, where the second book covers the spatial statistics R-package spatstat. Kroese and Botev also have a good introduction in the edited collection Stochastic Geometry, Spatial Statistics and Random Fields : Models and Algorithms by Schmidt, where the relevant chapter (number 12) is also freely available online.

More general stochastic simulation books that cover relevant material include Uniform Random Variate Generation by Devroye and Stochastic Simulation: Algorithms and Analysis by Asmussen and Glynn.