Tag: 3Blue1Brown

The Box-Muller method for simulating normal variables

In the previous post, I covered a simple but much used method for simulating random variables or, rather, generating random variates. To simulate a random variable, the method requires writing down, in a tractable manner, the inverse of its cumulative distribution function.

But in the case of the normal (or Gaussian) distribution, there is no closed-form expression for its cumulative distribution function nor its inverse. This means you cannot, in an elegant and fast way at least, generate with the inverse method a single normal random variable using a single uniform random variable.

Interestingly, however, you can generate two (independent) normal variables with two (independent) uniform variables using the Box-Muller method, originally proposed by George Box and Mervin E. Muller. This approach uses the inverse method, but in practice it’s not used much (see below). I detail this method because I find it neat and it highlights the connection between the normal distribution and rotational symmetry, which has been the subject of some recent 3Blue1Brown videos on YouTube.

(This method was also used to simulate the Thomas point process, which I covered in a previous post.)

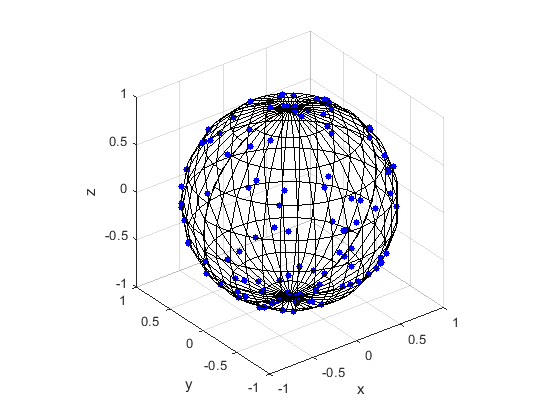
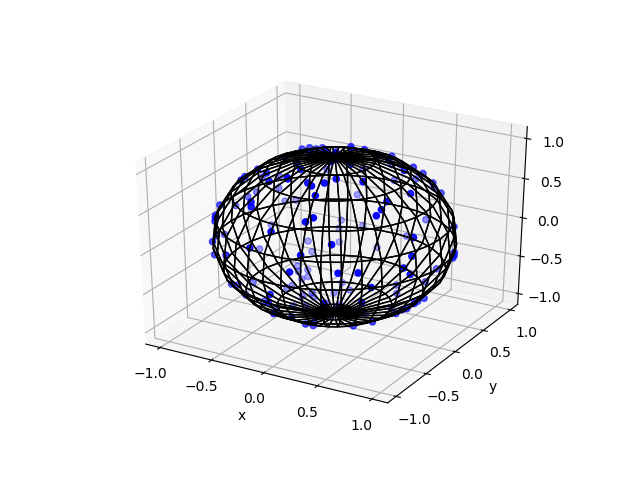
Incidentally, this connection is also mentioned in a previous post on simulating a Poisson point process on the surface of a sphere.  In that method post, Method 2 uses an observation by the Muller that normal random variables can be used to position points uniformly on spheres.

I imagine this method was first observed by transforming two normal variables, instead of guessing various distribution pairs that would work.  Then I’ll sketch the proof in the opposite direction, though it works in both directions.

Proof outline

The joint probability density of two independent variables is simply the product of the two individual probabilities densities. Then the joint density of two standard normal variables is

$$\begin{align}f_{X,Y}(x,y)&=\left[\frac{1}{\sqrt{2\pi}}e^{-x^2/2}\right]\left[\frac{1}{\sqrt{2\pi}}e^{-y^2/2}\right]\\&=\frac{1}{{2\pi}}e^{-(x^2+y^2)/2}\,.\end{align}$$

Now it requires a change of coordinates in two dimensions (from Cartesian to polar) using a Jacobian determinant, which in this case is \(|J(\theta,r)=r|\).1Alternatively, you can simply recall the so-called area element \(dA=r\,dr\,d\theta\).  giving a new joint probability density

$$f_{\Theta,R}(\theta,r)=\left[\frac{1}{\sqrt{2\pi}}\right]\left[ r\,e^{-r^2/2}\right]\,.$$

Now we just identify the two probability densities. The first probability density corresponds to a uniform variable on \([0, 2\pi]\), whereas the second is that of a Rayleigh variable with parameter \(\sigma=1\). Of course the proof works in the opposite direction because the transformation (between Cartesian and polar coordinates) is a one-to-one function.

Algorithm

Here’s the Box-Muller method for simulating two (independent) standard normal variables with two (independent) uniform random variables.

Two (independent) standard normal random variable \(Z_1\) and \(Z_2\)

  1. Generate two (independent) uniform random variables \(U_1\sim U(0,1)\) and \(U_2\sim U(0,1)\).
  2. Return \(Z_1=\sqrt{-2\ln U_1}\cos(2\pi U_2)\) and \(Z_2=\sqrt{-2\ln U_1}\sin(2\pi U_2)\).

The method effectively samples a uniform angular variable \(\Theta=2\pi U_2\) on the interval \([0,2\pi]\) and a radial variable \(R=\sqrt{-2\ln U_1}\) with a Rayleigh distribution.

The algorithm produces two independent standard normal variables. Of course, as many of us learn in high school, if \(Z\) is a standard normal variable, then the random variable \(X=\sigma Z +\mu\) is a normal variable with mean \(\mu\) and standard deviation \(\sigma>0\) .

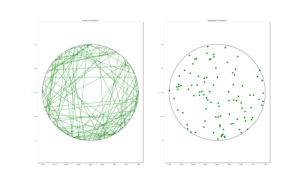
The Box-Muller method is rarely used

Sadly this method isn’t typically used, as historically computer processors were slow at doing the calculations, so other methods were employed such as the ziggurat algorithm. Also, although processors can now do such calculations much faster, many languages, not just scientific ones, come with functions for generating normal variables. Consequently, there’s not much need in implementing this method.

Further reading

Websites

Many websites detail this method. Here’s a couple:

Papers

The original paper (which is freely available here) is:

  • 1958 – Box and Muller, A Note on the Generation of Random Normal Deviates.

Another paper by Muller connects normal variables and the (surface of a) sphere:

  • 1959 – Muller, A note on a method for generating points uniformly on n-dimensional spheres.

Books

Many books on stochastic simulation cover the Box-Muller method. The classic book by Devroye with the descriptive title Non-Uniform Random Variate Generation covers this method; see Section 4.1. There’s also the Handbook of Monte Carlo Methods by Kroese, Taimre and Botev; see Section 3.1.2.7. Ripley also covers the method (and he makes a remark with some snark that many people incorrectly spell it the Box-Müller method); see Section 3.1. The book Stochastic Simulation: Algorithms and Analysis by Asmussen and Glynn also mention the method and a variation by Marsaglia; see Examples 2.11 and 2.12.

Simulating a Poisson point process on a sphere

In this post I’ll describe how to simulate or sample a homogeneous Poisson point process on the surface of a sphere. I have already simulated this point process on a rectangle, triangle disk, and circle.

Of course, by sphere, I mean the everyday object that is the surface of a three-dimensional ball, where this two-dimensional object is often denoted by \(S^2\).  Mathematically, this is a generalization from a Poisson point process on a circle, which is slightly simpler than randomly positioning points on a disk.  I recommend reading those two posts first, as a lot of the material presented here builds off them.

I have not needed such a simulation in my own work, but I imagine there are many reasons why you would want to simulate a Poisson point process on a sphere. As some motivation, we can imagine these points on a sphere representing, say, meteorites or lightning hitting the Earth.

The generating the number of points is not difficult. The trick is positioning the points on the sphere in a uniform way.  As is often the case, there are various ways to do this, and I recommend this post, which lists the main ones.  I will use two methods that I consider the most natural and intuitive ones, namely using spherical coordinates and normal random variables, which is what I did in the post on the circle.

Incidentally, a simple modification allows you to scatter the points uniformly inside the sphere, but you would typically say ball in mathematics, giving a Poisson point process inside a ball; see below for details.

Steps

As always, simulating a Poisson point process requires two steps.

Number of points

The number of points of a Poisson point process on the surface of a sphere of radius \(r>0\) is a Poisson random variable with mean \(\lambda S_2\), where \(S_2=4\pi r^2\) is the surface area of the sphere. (In this post I give some details for simulating or sampling Poisson random variables or, more accurately, variates.)

Locations of points

For any homogeneous Poisson point process, we need to position the points uniformly on the underlying space, which is in this case is the sphere. I will outline two different methods for positioning the points randomly and uniformly on a sphere.

Method 1: Spherical coordinates

The first method is based on spherical coordinates \((\rho, \theta,\phi)\), where the radial coordinate \(\rho\geq 0\), and the angular coordinates \(0 \leq \theta\leq 2\pi\) and \(0\leq \phi \leq \pi\). The change of coordinates gives \(x=\rho\sin(\theta)\cos(\phi)\), \(y=\rho\sin(\theta)\sin(\phi)\), and \(z=\rho\cos(\phi)\).

Now we use Proposition 1.1 in this paper. For each point, we generate two uniform variables \(V\) and \(\Theta\) on the respective intervals \((-1,1)\) and \((0,2\pi)\). Then we place the point with the Cartesian coordinates

$$X =  r  \sqrt{1-V^2} \cos\Theta, $$

$$Y =  r  \sqrt{1-V^2}\sin\Theta, $$

$$ Z=r V. $$

This method places a uniform point on a sphere with a radius \(r\).

How does it work?

I’ll skip the precise details, but give some interpretation of this method. The random variable \(\Phi := \arccos V\) is the \(\phi\)-coordinate of the uniform point, which implies \(\sin \Phi=\sqrt{1-V^2}\), due to basic trigonometric identities.  The area element in polar coordinates is \(dA = \rho^2 \sin\phi d\phi d\theta \), which is constant with respect to \(\theta\). After integrating with respect to \(\phi\),  we see that the random variable \(V=\cos\Phi\) needs to be uniform (instead of \(\Phi\)) to ensure the point is uniformly located on the surface.

Method 2: Normal random variables

For each point, we generate three standard normal or Gaussian random variables, say, \(W_x\), \(W_y\), and \(W_z\), which are independent of each other. (The term standard here means the normal random variables have mean \(\mu =0\) and standard deviation \(\sigma=1\).)  The three random variables are the Cartesian components of the random point. We rescale the components by the Euclidean norm, then multiply by the radius \(r\), giving

$$X=\frac{rW_x}{(W_x^2+W_y^2+W_z^2)^{1/2}},$$

$$Y=\frac{rW_y}{(W_x^2+W_y^2+W_z^2)^{1/2}},$$

$$Z=\frac{rW_z}{(W_x^2+W_y^2+W_z^2)^{1/2}}.$$

These are the Cartesian coordinates of a point uniformly scattered on a  sphere with radius \(r\) and a centre at the origin.

How does it work?

The procedure is somewhat like the Box-Muller transform in reverse. In the post on the circle setting,  I gave an outline of the proof, which I recommend reading. The joint density of the normal random variables is from a multivariate normal distribution with zero correlation. This joint density is constant on the sphere, implying that the angle of the point \((W_x, W_y, W_z)\) will be uniformly distributed.

The vector formed from the normal variables \((W_x, W_y,W_z)\) is a random variable with a chi distribution.  We can see that the vector from the origin to the point \((X,Y,Z)\) has length one, because we rescaled it with the Euclidean norm.

Plotting

Depending on your plotting software, the points may more resemble points on an ellipsoid than a sphere due to the different scaling of the x, y and z axes. To fix this in MATLAB, run the command: axis square. In Python, it’s not straightforward to do this, as it seems to lack an automatic function, so I have skipped it.

Results

I have presented some results produced by code written in MATLAB and Python. The blue points are the Poisson points on the sphere. I have used a surface plot (with clear faces) to illustrate the underling sphere in black.

MATLAB

Python

Note: The aspect ratio in 3-D Python plots tends to squash the sphere slightly, but it is a sphere.

Code

The code for all my posts is located online here. For this post, the code in MATLAB and Python is here.  In Python I used the library mpl_toolkits for doing 3-D plots.

Poisson point process inside the sphere

Perhaps you want to simulate a Poisson point process inside the ball.  There are different ways we can do this, but I will describe just one way, which builds off Method 1 for positioning the points uniformly. (In a later post, I will modify Method 2, giving a way to uniformly position points inside the ball.)

For this simulation method, you need to make two simple modifications to the simulation procedure.

Number of points

The number of points of a Poisson point process inside a sphere of radius \(r>0\) is a Poisson random variable with mean \(\lambda V_3\), where \(V_3=4\pi r^3\) is the volume of the sphere.

Locations of points

We will modify Method 1 as outlined above. To sample the points uniformly in the sphere, you need to generate uniform variables on the unit interval \((0,1)\), take their cubic roots, and then, multiply them by the radius \(r\). (This is akin to the step of taking the square root in the disk setting.) The random variables for the angular coordinates are generated as before.

Further reading

I recommend this blog post, which discusses different methods for randomly placing points on spheres and inside spheres (or, rather, balls) in a uniform manner.  (Embedded in two dimensions, a sphere is a circle and a ball is a disk.)

Our Method 2 for positioning points uniformly, which uses normal variables, comes from the paper:

  • 1959, Muller, A note on a method for generating points uniformly on n-dimensional spheres.

This sampling method relies upon old observations that normal variables are connected to spheres and circles. I also found this post on a similar topic. Perhaps not surprisingly, the above paper is written by the same Muller behind the Box-Muller method for sampling normal random variables.

Update: The connection between the normal distribution and rotational symmetry has been the subject of some recent 3Blue1Brown videos on YouTube.

Here is some sample Python code for creating a 3-D scatter plot.

The Bertrand paradox

Mathematical paradoxes are results or observations in mathematics that are (seemingly) conflicting, unintuitive, incomprehensible, or just plain bizarre. They come in different flavours, such as those that play with notions of infinity, which means they often make little or no sense in a physical world. Other paradoxes, particularly those in probability, serve as a lesson that the problem needs to be posed in a precise manner. The Bertrand paradox is one of these.

Joseph Bertrand posed the original problem in his 1889 book Calcul des probabilités, which is available online (in French); page 4, Section 5. It’s a great illustrative problem involving simple probability and geometry, so it often appears in literature on the (closely related) mathematical fields of geometric probability and integral geometry.

Based on constructing a random chord in a circle, Bertrand’s paradox involves a single mathematical problem with three reasonable but different solutions. It’s less a paradox and more a cautionary tale. It’s really asking the question: What exactly do you mean by random?

Consequently, over the years the Bertrand paradox has inspired debate, with papers arguing what the true solution is. I recently discovered it has even inspired some passionate remarks on the internet; read the comments at www.bertrands-paradox.com.

Update: The people from Numberphile and 3Blue1Brown have recently produced a video on YouTube describing and explaining the Bertrand paradox.

But I am less interested in the different interpretations or philosophies of the problem. Rather, I want to simulate the three solutions. This is not very difficult, provided some trigonometry and knowledge from a previous post, where I describe how to simulate a (homogeneous) Poisson point process on the disk.

I won’t try to give a thorough analysis of the solutions, as there are much better websites doing that. For example, this MIT website gives a colourful explanation with pizza and fire-breathing monsters. The Wikipedia article also gives a detailed though less creative explanation for the three solutions.

My final code in MATLAB, R and Python code is located here.

The Problem

Bertrand considered a circle with an equilateral triangle inscribed it. If a chord in the circle is randomly chosen, what is the probability that the chord is longer than a side of the equilateral triangle?

The Solution(s)

Bertrand argued that there are three natural but different methods to randomly choose a chord, giving three distinct answers. (Of course, there are other methods, but these are arguably not the natural ones that first come to mind.)

Method 1: Random endpoints

On the circumference of the circle two points are randomly (that is, uniformly and independently) chosen, which are then used as the two endpoints of the chord.

The probability of this random chord being longer than a side of the triangle is one third.

Method 2: Random radius

A radius of the circle is randomly chosen (so the angle is chosen uniformly), then a point is randomly (also uniformly) chosen along the radius, and then a chord is constructed at this point so it is perpendicular to the radius.

The probability of this random chord being longer than a side of the triangle is one half.

Method 3: Random midpoint

A point is randomly (so uniformly) chosen in the circle, which is used as the midpoint of the chord, and the chord is randomly (also uniformly) rotated.

The probability of this random chord being longer than a side of the triangle is one quarter.

Simulation

All three answers involve randomly and independently sampling two random variables, and then doing some simple trigonometry. The setting naturally inspires the use of polar coordinates. I assume the circle has a radius \(r\) and a centre at the origin \(o\). I’ll arbitrarily number the end points one and two.

In all three solutions we need to generate uniform random variables on the interval \((0, 2\pi)\) to simulate random angles. I have already done this a couple of times in previous posts such as this one.

Method 1: Random endpoints

This is probably the most straightforward solution to simulate. We just need to simulate two uniform random variables \(\Theta_1\) and \(\Theta_2\) on the interval \((0, 2\pi)\) to describe the angles of the two points.

The end points of the chord (in Cartesian coordinates) are then simply:

Point 1: \(X_1=r \cos \Theta_1\), \(Y_1=r \sin \Theta_1\),

Point 2: \(X_2=r \cos \Theta_2\), \(Y_2=r \sin \Theta_2\).

Method 2: Random radius

This method also involves generating two uniform random variables. One random variable \(\Theta\) is for the angle, while the other \(P\) is the random radius, which means generating the random variable \(P\) on the interval \((0, r)\).

I won’t go into the trigonometry, but the random radius and its perpendicular chord create a right-angle triangle. The distance from the point \((\Theta, P)\) to the circle along the chord is:

$$Q=\sqrt{r^2-P^2}.$$

The endpoints of the chord are then:

Point 1: \(X_1=P \cos \Theta+ Q\sin \Theta\), \(Y_1= P \sin \Theta- Q\cos \Theta\),

Point 2: \(X_2=P \cos \Theta- Q\sin \Theta\), \(Y_2= P \sin \Theta+Q \cos \Theta\).

Take note of the signs in these expressions.

Method 3: Random midpoint

This method requires placing a point uniformly on a disk, which is also done when simulating a homogeneous Poisson point process on a disk, and requires two random variables \(\Theta’\) and \(P’\). Again, the angular random variable \(\Theta’\) is uniform.

The other random variable \(P’\) is not uniform. For \(P’\), we generate a random uniform variable on the unit interval \((0,1)\), and then we take the square root of it. We then multiply it by the radius, generating a random variable between \(0\) and \(r\). (We must take the square root because the area element of a sector is proportional to the radius squared, and not the radius.) The distribution of this random variable is an example of the triangular distribution.

The same trigonometry from Method 2 applies here, which gives the endpoints of the chord as:

Point 1: \(X_1=P’ \cos \Theta’+ Q’\sin \Theta’\), \(Y_1= P’ \sin \Theta’- Q’\cos \Theta’\),

Point 2: \(X_2=P’\cos \Theta’- Q’\sin \Theta’\), \(Y_2= P’\sin \Theta’+Q’ \cos \Theta’\),

where \(Q’:=\sqrt{r^2-{P’}^2}\). Again, take note of the signs in these expressions.

Results

To illustrate how the three solutions are different, I’ve plotted a hundred random line segments and their midpoints side by side. Similar plots are in the Wikipedia article.

Method 1: Random endpoints
Method 2: Random radius

Method 3: Random midpoint

Conclusion

For the chord midpoints, we know and can see that Method 3 gives uniform points, while Method 2 has a concentration of midpoints around the circle centre. Method 1 gives results that seem to somewhere between Method 2 and 3 in terms of clustering around the circle centre.

For the chords, we see that Method 3 results in fewer chords passing through the circle centre. Methods 1 and 2 seem to give a similar number of lines passing through this central region.

It’s perhaps hard to see, but it can be shown that Method 2 gives the most uniform results. By this, I mean that the number of lines and their orientations statistically do not vary in different regions of the circle.

We can now position random lines in uniform manner. All we need now is a Poisson number of lines to generate something known as a Poisson line process, which will be the subject of the next post.

Further reading

I’ve already mentioned that there are some good websites on the topic of the Bertrand paradox. For example:

www.bertrands-paradox.com

web.mit.edu/tee/www/bertrand

www.cut-the-knot.org/bertrand.shtml

mathworld.wolfram.com/BertrandsProblem.html

Various authors have mentioned or discussed the Bertrand paradox in books on the related subjects of geometric probability, integral geometry and stochastic geometry. A good and recent introduction is given by Calka in Section 1.3 of the published lectures Stochastic Geometry: Modern Research Frontiers.

Other classic books that cover the topic including, for example, see Problem 1.2 in Geometrical Probability by Kendall and Moran. (Despite Maurice G. Kendall writing a book on geometric probability, he was not related to stochastic geometry pioneer David G Kendall.) It’s also discussed on page 44 in Geometric Probability by Solomon. For a book that involves more advance knowledge of geometry and (abstract) algebra, see Chapter 3 in Integral Geometry and Geometric Probability by Santaló.

The Bertrand paradox is also in The Pleasures of Probability by Isaac. It’s covered in a non-mathematical way in the book Paradoxes from A to Z by Clark. Edwin Jaynes studied the problem and proposed a solution in a somewhat famous 1973 paper, titled The Well-Posed Problem.

The original problem can be read in French in Bertrand’s work, which is available online here or here (starting at the bottom of page 4).

Code

The MATLAB, R and Python code can be found here. In the code, I have labelled the methods A, B and C instead 1, 2 and 3.