Tag: circle

Simulating a Poisson point process on a n-dimensional sphere

In the previous post I outlined how to simulate or sample a homogeneous Poisson point process on the surface of a sphere. Now I will consider a homogeneous Poisson point process on the \((n-1)-\) sphere, which is the surface of the Euclidean ball in \(n\) dimensions.

This is a short post because it immediately builds off the previous post. For positioning the points uniformly, I will use Method 2 from that post, which uses normal random variables, as it immediately gives a fast method in \(n\) dimensions.

I wrote this post and the code more for curiosity than any immediate application. But simulating a Poisson point process in this setting requires placing points uniformly on a sphere. And there are applications in that, such as Monte Carlo integration methods, as mentioned in this post, which nicely details different sampling methods.

Steps

As is the case for other shapes, simulating a Poisson point process requires two steps.

Number of points

The number of points of a Poisson point process on the surface of a sphere of radius \(r>0\) is a Poisson random variable. The mean of this random variable is \(\lambda S_{n-1}\), where \(S_{n-1}\) is the surface area of the sphere.  For a ball embedded in \(n\) dimension, the area of the corresponding sphere is given by

$$S_{n-1} = \frac{2 \pi ^{n/2}  }{\Gamma(n/2)} r^{n-1},$$

where \(\Gamma\) is the gamma function, which is a natural generalization of the factorial. In MATLAB, we can simply use the function gamma.  In Python, we need to use the SciPy function scipy.special. gamma.

Locations of points

For each point on the sphere, we generate \(n\) standard normal or Gaussian random variables, say, \(W_1, \dots, W_n\), which are independent of each other. These random variables are the Cartesian components of the random point. We rescale the components by the Euclidean norm, then multiply by the radius \(r\).

For \(i=1,\dots, n\), we obtain

$$X_i=\frac{rW_i}{(W_1^2+\cdots+W_n^2)^{1/2}}.$$

These are the Cartesian coordinates of a point uniformly scattered on a  sphere with radius \(r\) and a centre at the origin.

How does it work?

In the post on the circle setting, I gave a more detailed outline of the proof, where I said the method is like the Box-Muller transform in reverse. The joint density of the normal random variables is from a multivariate normal distribution with zero correlation. This joint density a function of the Cartesian equation for a sphere. This means the density is constant on the sphere, implying that the angle of the point \((W_1,\dots, W_n)\) will be uniformly distributed.

The vector formed from the normal variables \((W_1,\dots,W_n)\) is a random variable with a chi distribution.  But the final vector, which stretches from the origin to the point \((X_1,\dots,X_n)\), has length one, because we rescaled it with the Euclidean norm.

Code

The code for all my posts is located online here. For this post, the code in MATLAB and Python is here.

Further reading

I recommend this blog post, which discusses different methods for randomly placing points on spheres and inside spheres (or, rather, balls) in a uniform manner.  (Embedded in two dimensions, a sphere is a circle and a ball is a disk.)

Our Method 2 for positioning points uniformly, which uses normal variables, comes from the paper:

  • 1959, Muller, A note on a method for generating points uniformly on n-dimensional spheres.

Two recent works on this approach are the papers:

  • 2010, Harman and Lacko, On decompositional algorithms for uniform sampling from -spheres and -balls;
  • 2017, Voelker, Gosman, Stewart, Efficiently sampling vectors and coordinates.

Simulating a Poisson point process on a sphere

In this post I’ll describe how to simulate or sample a homogeneous Poisson point process on the surface of a sphere. I have already simulated this point process on a rectangle, triangle disk, and circle.

Of course, by sphere, I mean the everyday object that is the surface of a three-dimensional ball, where this two-dimensional object is often denoted by \(S^2\).  Mathematically, this is a generalization from a Poisson point process on a circle, which is slightly simpler than randomly positioning points on a disk.  I recommend reading those two posts first, as a lot of the material presented here builds off them.

I have not needed such a simulation in my own work, but I imagine there are many reasons why you would want to simulate a Poisson point process on a sphere. As some motivation, we can imagine these points on a sphere representing, say, meteorites or lightning hitting the Earth.

The generating the number of points is not difficult. The trick is positioning the points on the sphere in a uniform way.  As is often the case, there are various ways to do this, and I recommend this post, which lists the main ones.  I will use two methods that I consider the most natural and intuitive ones, namely using spherical coordinates and normal random variables, which is what I did in the post on the circle.

Incidentally, a simple modification allows you to scatter the points uniformly inside the sphere, but you would typically say ball in mathematics, giving a Poisson point process inside a ball; see below for details.

Steps

As always, simulating a Poisson point process requires two steps.

Number of points

The number of points of a Poisson point process on the surface of a sphere of radius \(r>0\) is a Poisson random variable with mean \(\lambda S_2\), where \(S_2=4\pi r^2\) is the surface area of the sphere. (In this post I give some details for simulating or sampling Poisson random variables or, more accurately, variates.)

Locations of points

For any homogeneous Poisson point process, we need to position the points uniformly on the underlying space, which is in this case is the sphere. I will outline two different methods for positioning the points randomly and uniformly on a sphere.

Method 1: Spherical coordinates

The first method is based on spherical coordinates \((\rho, \theta,\phi)\), where the radial coordinate \(\rho\geq 0\), and the angular coordinates \(0 \leq \theta\leq 2\pi\) and \(0\leq \phi \leq \pi\). The change of coordinates gives \(x=\rho\sin(\theta)\cos(\phi)\), \(y=\rho\sin(\theta)\sin(\phi)\), and \(z=\rho\cos(\phi)\).

Now we use Proposition 1.1 in this paper. For each point, we generate two uniform variables \(V\) and \(\Theta\) on the respective intervals \((-1,1)\) and \((0,2\pi)\). Then we place the point with the Cartesian coordinates

$$X =  r  \sqrt{1-V^2} \cos\Theta, $$

$$Y =  r  \sqrt{1-V^2}\sin\Theta, $$

$$ Z=r V. $$

This method places a uniform point on a sphere with a radius \(r\).

How does it work?

I’ll skip the precise details, but give some interpretation of this method. The random variable \(\Phi := \arccos V\) is the \(\phi\)-coordinate of the uniform point, which implies \(\sin \Phi=\sqrt{1-V^2}\), due to basic trigonometric identities.  The area element in polar coordinates is \(dA = \rho^2 \sin\phi d\phi d\theta \), which is constant with respect to \(\theta\). After integrating with respect to \(\phi\),  we see that the random variable \(V=\cos\Phi\) needs to be uniform (instead of \(\Phi\)) to ensure the point is uniformly located on the surface.

Method 2: Normal random variables

For each point, we generate three standard normal or Gaussian random variables, say, \(W_x\), \(W_y\), and \(W_z\), which are independent of each other. (The term standard here means the normal random variables have mean \(\mu =0\) and standard deviation \(\sigma=1\).)  The three random variables are the Cartesian components of the random point. We rescale the components by the Euclidean norm, then multiply by the radius \(r\), giving

$$X=\frac{rW_x}{(W_x^2+W_y^2+W_z^2)^{1/2}},$$

$$Y=\frac{rW_y}{(W_x^2+W_y^2+W_z^2)^{1/2}},$$

$$Z=\frac{rW_z}{(W_x^2+W_y^2+W_z^2)^{1/2}}.$$

These are the Cartesian coordinates of a point uniformly scattered on a  sphere with radius \(r\) and a centre at the origin.

How does it work?

The procedure is somewhat like the Box-Muller transform in reverse. In the post on the circle setting,  I gave an outline of the proof, which I recommend reading. The joint density of the normal random variables is from a multivariate normal distribution with zero correlation. This joint density is constant on the sphere, implying that the angle of the point \((W_x, W_y, W_z)\) will be uniformly distributed.

The vector formed from the normal variables \((W_x, W_y,W_z)\) is a random variable with a chi distribution.  We can see that the vector from the origin to the point \((X,Y,Z)\) has length one, because we rescaled it with the Euclidean norm.

Plotting

Depending on your plotting software, the points may more resemble points on an ellipsoid than a sphere due to the different scaling of the x, y and z axes. To fix this in MATLAB, run the command: axis square. In Python, it’s not straightforward to do this, as it seems to lack an automatic function, so I have skipped it.

Results

I have presented some results produced by code written in MATLAB and Python. The blue points are the Poisson points on the sphere. I have used a surface plot (with clear faces) to illustrate the underling sphere in black.

MATLAB

Python

Note: The aspect ratio in 3-D Python plots tends to squash the sphere slightly, but it is a sphere.

Code

The code for all my posts is located online here. For this post, the code in MATLAB and Python is here.  In Python I used the library mpl_toolkits for doing 3-D plots.

Poisson point process inside the sphere

Perhaps you want to simulate a Poisson point process inside the ball.  There are different ways we can do this, but I will describe just one way, which builds off Method 1 for positioning the points uniformly. (In a later post, I will modify Method 2, giving a way to uniformly position points inside the ball.)

For this simulation method, you need to make two simple modifications to the simulation procedure.

Number of points

The number of points of a Poisson point process inside a sphere of radius \(r>0\) is a Poisson random variable with mean \(\lambda V_3\), where \(V_3=4\pi r^3\) is the volume of the sphere.

Locations of points

We will modify Method 1 as outlined above. To sample the points uniformly in the sphere, you need to generate uniform variables on the unit interval \((0,1)\), take their cubic roots, and then, multiply them by the radius \(r\). (This is akin to the step of taking the square root in the disk setting.) The random variables for the angular coordinates are generated as before.

Further reading

I recommend this blog post, which discusses different methods for randomly placing points on spheres and inside spheres (or, rather, balls) in a uniform manner.  (Embedded in two dimensions, a sphere is a circle and a ball is a disk.)

Our Method 2 for positioning points uniformly, which uses normal variables, comes from the paper:

  • 1959, Muller, A note on a method for generating points uniformly on n-dimensional spheres.

This sampling method relies upon old observations that normal variables are connected to spheres and circles. I also found this post on a similar topic. Perhaps not surprisingly, the above paper is written by the same Muller behind the Box-Muller method for sampling normal random variables.

Update: The connection between the normal distribution and rotational symmetry has been the subject of some recent 3Blue1Brown videos on YouTube.

Here is some sample Python code for creating a 3-D scatter plot.

Simulating a Poisson point process on a circle

In this post, I’ll take a break from the more theoretical posts. Instead I’ll describe how to simulate or sample a homogeneous Poisson point process on a circle.  I have already simulated this point process on a rectangle, triangle and disk. In some sense, I should have done this simulation method before the disk one, as it’s easier to simulate. I recommend reading that post first, as the material presented here builds off it.

Sampling a homogeneous Poisson point process on a circle is rather straightforward.  It just requires using a fixed radius and uniformly choose angles from interval \((0, 2\pi)\). But the circle setting gives an opportunity to employ a different method for positioning points uniformly on circles and, more generally, spheres. This approach uses Gaussian random variables, and it becomes much more efficient when the points are placed on high dimensional spheres.

Steps

Simulating a Poisson point process requires two steps: simulating the random number of points and then randomly positioning each point.

Number of points

The number of points of a Poisson point process on circle of radius \(r>0\) is a Poisson random variable with mean \(\lambda C\), where \(C=2\pi r\) is the circumference of the circle.  You just need to be able to need to produce (pseudo-)random numbers according to a Poisson distribution.

To generate Poisson variables in MATLAB,  use the poissrnd function with the argument \(\lambda C\).  In Python, use either the scipy.stats.poisson or numpy.random.poisson function from the SciPy or NumPy libraries. (If you’re curious how Poisson simulation works, I suggest seeing this post for details on sampling Poisson random variables or, more accurately, variates.)

Locations of points

For a homogeneous Poisson point process, we need to uniformly position points on the underlying space, which is this case is a circle. We will look at two different ways to position points uniformly on a circle. The first is arguably the most natural approach.

Method 1: Polar coordinates

We use polar coordinates due to the nature of the problem. To position all the points uniformly on a circle, we simple generate uniform numbers on the unit interval \((0,1)\). We then multiply these random numbers by \(2\pi\).

We have generated polar coordinates for points uniformly located on the circle. To plot the points, we have to convert the coordinates back to Cartesian form by using the change of coordinates:  \(x=\rho\cos(\theta)\) and \(y=\rho\sin(\theta)\).

Method 2: Normal random variables

For each point, we generate two standard normal or Gaussian random variables, say, \(W_x\) and \(W_y\), which are independent of each other. (The term standard here means the normal random variables have mean \(\mu =0\) and standard deviation \(\sigma=1\).) These two random variables are the Cartesian components of a random point.  We then rescale the two values by the Euclidean norm, giving

$$X=\frac{W_x}{(W_x^2+W_y^2)^{1/2}},$$

$$Y=\frac{W_y}{(W_x^2+W_y^2)^{1/2}}.$$

These are the Cartesian coordinates of points uniformly scattered around a unit circle with centre at the origin. We multiply the two random values \(X\) and \(Y\) by the \(r>0\)  for a circle with radius \(r\).

How does it work?

The procedure is somewhat like the Box-Muller transform in reverse. I’ll give an outline of the proof. The joint density of the random variables \(W_x\) and \(W_y\) is that of the bivariate normal distribution with zero correlation, meaning it has the joint density

$$ f(x,y)=\frac{1}{2\pi}e^{[-(x^2+y^2)/2]}.$$

We see that the function \(f\) is a constant when we trace around any line for which \((x^2+y^2)\) is a constant, which is simply the Cartesian equation for a circle (where the radius is the square root of the aforementioned constant). This means that the angle of the point \((W_x, W_y)\) will be uniformly distributed.

Now we just need to look at the distance of the random point. The vector formed from the pair of normal variables \((W_x, W_y)\) is a Rayleigh random variable.  We can see that the vector from the origin to the point \((X,Y)\) has length one, because we rescaled it with the Euclidean norm.

Results

I have presented some results produced by code written in MATLAB and Python. The blue points are the Poisson points on the sphere. I have used a surface plot (with clear faces) in black to illustrate the underling sphere.

MATLAB

Python

Code

The code for all my posts is located online here. For this post, the code in MATLAB and Python is here.

Further reading

I recommend this blog post, which discusses different methods for randomly placing points on spheres and inside spheres (or, rather, balls) in a uniform manner.  (Embedded in two dimensions, a sphere is a circle and a ball is a disk.) A key paper on using normal variables is the following:

  • 1959, Muller, A note on a method for generating points uniformly on n-dimensional spheres.

As I mentioned in the post on the disk, the third edition of the classic book Stochastic Geometry and its Applications by Chiu, Stoyan, Kendall and Mecke details on page 54 how to uniformly place points on a disk.  It just requires a small modification for the circle.

Simulating a Poisson line process

Instead of points, we can consider other objects randomly scattered on some underlying mathematical space. If we take a Poisson point process, then we can use (infinitely long) straight lines instead of points, giving a Poisson line process. Researchers have studied and used this random object to model physical phenomena. In this post I’ll cover how to simulate a homogeneous Poisson line process in MATLAB, R and Python. The code can be downloaded from here. 

Overview

For simulating a Poisson line process, the key question is how to randomly position the lines.  This is related to a classic problem in probability theory called the Bertrand paradox.  I discussed this illustration in probability in a previous post, where I also included code for simulating it. I highly recommend reading that post first.

The Bertrand paradox involves three methods for positioning random lines. We use Method 2 to achieve a uniform positioning of lines, meaning the number of lines and orientation of lines is statistically uniform. Then it also makes sense to use this method for simulating a homogeneous (or uniform) Poisson line process.  

We can interpret a line process as a point process. For a line process on the plane \(\textbf{R}^2\), it can be described by a point process on \((0,\infty)\times (0,2\pi)\), which is an an infinitely long cylinder. In other words, the Poisson line process can be described as a Poisson point process.

For simulating a Poisson line process, it turns out the disk is the most natural setting. (Again, this goes back to the Bertrand paradox.) More specifically, how the (infinitely long) lines intersect a disk of a fixed radius \(r>0\). The problem of simulating a Poisson line process reduces to randomly placing chords in a disk. For other simulation windows in the plane, we can always bound any non-circular region with a sufficiently large disk.

Steps

Number of lines

Of course, with all things Poisson, the number of lines will be  a Poisson random variable, but what will its parameter be? This homogeneous (or uniform) Poisson line process forms a one-dimensional homogeneous (or uniform) Poisson point process around the edge of the disk with a circumference \(2 \pi r \). Then the number of lines is simply a Poisson variable with parameter \(\lambda 2 \pi r \).

Locations of points

To position a single line uniformly in a disk, we need to generate two uniform random variables. One random variable gives the angle describing orientation of the line, so it’s a uniform random variable \(\Theta\) on the interval \((0,2\pi)\). 

The other random variable gives the distance from the origin to the disk edge, meaning it’s a uniform random variable \(P\) on the interval \((0,r)\), where \(r\) is the radius of the disk.  The random radius and its perpendicular chord create a right-angle triangle.  The distance from the point \((\Theta, P)\) to the disk edge (that is, the circle) along the chord is:

$$Q=\sqrt{r^2-P^2}.$$

The endpoints of the chord (that is, the points on the disk edge) are then:

Point 1: \(X_1=P \cos \Theta+ Q\sin \Theta\), \(Y_1= P \sin \Theta- Q\cos \Theta\),

Point 2: \(X_2=P \cos \Theta- Q\sin \Theta\), \(Y_2= P \sin \Theta+Q \cos \Theta\).

Code

I have implemented the simulation procedure in MATLAB, R and Python, which, as usual, are all very similar. I haven’t put my code here, because the software behind my website keeps mangling it.  As always, I have uploaded my code to a repository; for this post, it’s in this directory.

I have written the code in R, but I wouldn’t use it in general. That’s because if you’re using R, then, as I have said before, I strongly recommend using the powerful spatial statistics library spatstat. For a simulating Poisson line process, there’s the function rpoisline.  

The chief author of spatstat, Adrian Baddeley, has written various lectures and books on the related topics of point processes, spatial statistics, and geometric probability. In this post, he answered why the angular coordinates have to be chosen uniformly. 

Results

MATLAB

R

Python

Further reading

To read about the Poisson line process, it’s best to start with the Bertrand problem, which is covered in many works on geometric probability and related fields. A good and recent introduction is given by Calka in (Section 1.3) of the lectures titled Stochastic Geometry: Modern Research Frontiers, which were edited by Coupier and published by Springer.  Also see, for example, problem 1.2 in Geometrical Probability by Kendall and Moran or page 44 in Geometric Probability by Solomon.  

For the Poisson line process, I highly recommend Section 7.2 in the monograph Poisson Processes by Kingman. Also see Example 8.2 in the standard textbook Stochastic Geometry and its Applications by Chiu, Stoyan, Kendall and Mecke. The Poisson line process book also appears in Exercise 5.2 in the book Stochastic Simulation – Algorithms and Analysis by Asmussen and Glynn. 

For online resources, this set of lectures by Christian Lantuéjoul
covers the Poisson line process. Wilfrid Kendall covers the Poisson line process in this talk in relation to so-called Poisson cities. 

The Bertrand paradox

Mathematical paradoxes are results or observations in mathematics that are (seemingly) conflicting, unintuitive, incomprehensible, or just plain bizarre. They come in different flavours, such as those that play with notions of infinity, which means they often make little or no sense in a physical world. Other paradoxes, particularly those in probability, serve as a lesson that the problem needs to be posed in a precise manner. The Bertrand paradox is one of these.

Joseph Bertrand posed the original problem in his 1889 book Calcul des probabilités, which is available online (in French); page 4, Section 5. It’s a great illustrative problem involving simple probability and geometry, so it often appears in literature on the (closely related) mathematical fields of geometric probability and integral geometry.

Based on constructing a random chord in a circle, Bertrand’s paradox involves a single mathematical problem with three reasonable but different solutions. It’s less a paradox and more a cautionary tale. It’s really asking the question: What exactly do you mean by random?

Consequently, over the years the Bertrand paradox has inspired debate, with papers arguing what the true solution is. I recently discovered it has even inspired some passionate remarks on the internet; read the comments at www.bertrands-paradox.com.

Update: The people from Numberphile and 3Blue1Brown have recently produced a video on YouTube describing and explaining the Bertrand paradox.

But I am less interested in the different interpretations or philosophies of the problem. Rather, I want to simulate the three solutions. This is not very difficult, provided some trigonometry and knowledge from a previous post, where I describe how to simulate a (homogeneous) Poisson point process on the disk.

I won’t try to give a thorough analysis of the solutions, as there are much better websites doing that. For example, this MIT website gives a colourful explanation with pizza and fire-breathing monsters. The Wikipedia article also gives a detailed though less creative explanation for the three solutions.

My final code in MATLAB, R and Python code is located here.

The Problem

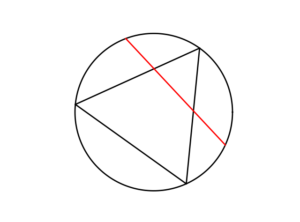
Bertrand considered a circle with an equilateral triangle inscribed it. If a chord in the circle is randomly chosen, what is the probability that the chord is longer than a side of the equilateral triangle?

The Solution(s)

Bertrand argued that there are three natural but different methods to randomly choose a chord, giving three distinct answers. (Of course, there are other methods, but these are arguably not the natural ones that first come to mind.)

Method 1: Random endpoints

On the circumference of the circle two points are randomly (that is, uniformly and independently) chosen, which are then used as the two endpoints of the chord.

The probability of this random chord being longer than a side of the triangle is one third.

Method 2: Random radius

A radius of the circle is randomly chosen (so the angle is chosen uniformly), then a point is randomly (also uniformly) chosen along the radius, and then a chord is constructed at this point so it is perpendicular to the radius.

The probability of this random chord being longer than a side of the triangle is one half.

Method 3: Random midpoint

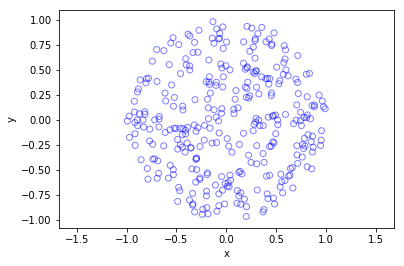
A point is randomly (so uniformly) chosen in the circle, which is used as the midpoint of the chord, and the chord is randomly (also uniformly) rotated.

The probability of this random chord being longer than a side of the triangle is one quarter.

Simulation

All three answers involve randomly and independently sampling two random variables, and then doing some simple trigonometry. The setting naturally inspires the use of polar coordinates. I assume the circle has a radius \(r\) and a centre at the origin \(o\). I’ll arbitrarily number the end points one and two.

In all three solutions we need to generate uniform random variables on the interval \((0, 2\pi)\) to simulate random angles. I have already done this a couple of times in previous posts such as this one.

Method 1: Random endpoints

This is probably the most straightforward solution to simulate. We just need to simulate two uniform random variables \(\Theta_1\) and \(\Theta_2\) on the interval \((0, 2\pi)\) to describe the angles of the two points.

The end points of the chord (in Cartesian coordinates) are then simply:

Point 1: \(X_1=r \cos \Theta_1\), \(Y_1=r \sin \Theta_1\),

Point 2: \(X_2=r \cos \Theta_2\), \(Y_2=r \sin \Theta_2\).

Method 2: Random radius

This method also involves generating two uniform random variables. One random variable \(\Theta\) is for the angle, while the other \(P\) is the random radius, which means generating the random variable \(P\) on the interval \((0, r)\).

I won’t go into the trigonometry, but the random radius and its perpendicular chord create a right-angle triangle. The distance from the point \((\Theta, P)\) to the circle along the chord is:

$$Q=\sqrt{r^2-P^2}.$$

The endpoints of the chord are then:

Point 1: \(X_1=P \cos \Theta+ Q\sin \Theta\), \(Y_1= P \sin \Theta- Q\cos \Theta\),

Point 2: \(X_2=P \cos \Theta- Q\sin \Theta\), \(Y_2= P \sin \Theta+Q \cos \Theta\).

Take note of the signs in these expressions.

Method 3: Random midpoint

This method requires placing a point uniformly on a disk, which is also done when simulating a homogeneous Poisson point process on a disk, and requires two random variables \(\Theta’\) and \(P’\). Again, the angular random variable \(\Theta’\) is uniform.

The other random variable \(P’\) is not uniform. For \(P’\), we generate a random uniform variable on the unit interval \((0,1)\), and then we take the square root of it. We then multiply it by the radius, generating a random variable between \(0\) and \(r\). (We must take the square root because the area element of a sector is proportional to the radius squared, and not the radius.) The distribution of this random variable is an example of the triangular distribution.

The same trigonometry from Method 2 applies here, which gives the endpoints of the chord as:

Point 1: \(X_1=P’ \cos \Theta’+ Q’\sin \Theta’\), \(Y_1= P’ \sin \Theta’- Q’\cos \Theta’\),

Point 2: \(X_2=P’\cos \Theta’- Q’\sin \Theta’\), \(Y_2= P’\sin \Theta’+Q’ \cos \Theta’\),

where \(Q’:=\sqrt{r^2-{P’}^2}\). Again, take note of the signs in these expressions.

Results

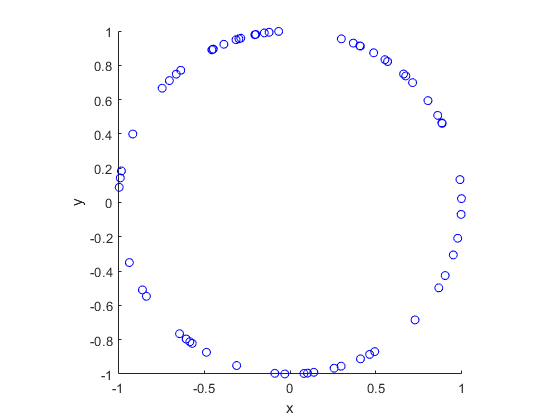
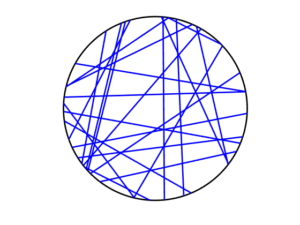
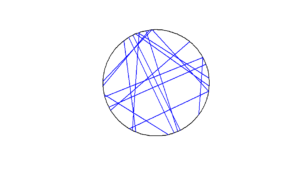
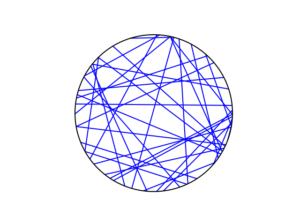
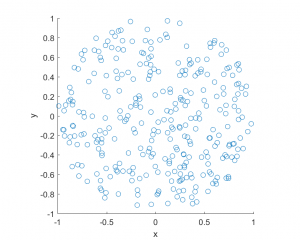
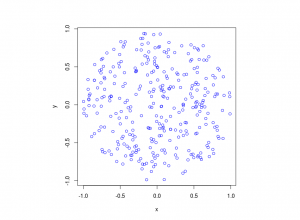
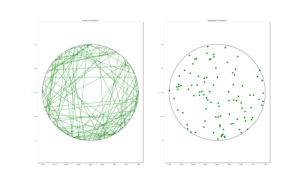
To illustrate how the three solutions are different, I’ve plotted a hundred random line segments and their midpoints side by side. Similar plots are in the Wikipedia article.

Method 1: Random endpoints
Method 2: Random radius

Method 3: Random midpoint

Conclusion

For the chord midpoints, we know and can see that Method 3 gives uniform points, while Method 2 has a concentration of midpoints around the circle centre. Method 1 gives results that seem to somewhere between Method 2 and 3 in terms of clustering around the circle centre.

For the chords, we see that Method 3 results in fewer chords passing through the circle centre. Methods 1 and 2 seem to give a similar number of lines passing through this central region.

It’s perhaps hard to see, but it can be shown that Method 2 gives the most uniform results. By this, I mean that the number of lines and their orientations statistically do not vary in different regions of the circle.

We can now position random lines in uniform manner. All we need now is a Poisson number of lines to generate something known as a Poisson line process, which will be the subject of the next post.

Further reading

I’ve already mentioned that there are some good websites on the topic of the Bertrand paradox. For example:

www.bertrands-paradox.com

web.mit.edu/tee/www/bertrand

www.cut-the-knot.org/bertrand.shtml

mathworld.wolfram.com/BertrandsProblem.html

Various authors have mentioned or discussed the Bertrand paradox in books on the related subjects of geometric probability, integral geometry and stochastic geometry. A good and recent introduction is given by Calka in Section 1.3 of the published lectures Stochastic Geometry: Modern Research Frontiers.

Other classic books that cover the topic including, for example, see Problem 1.2 in Geometrical Probability by Kendall and Moran. (Despite Maurice G. Kendall writing a book on geometric probability, he was not related to stochastic geometry pioneer David G Kendall.) It’s also discussed on page 44 in Geometric Probability by Solomon. For a book that involves more advance knowledge of geometry and (abstract) algebra, see Chapter 3 in Integral Geometry and Geometric Probability by Santaló.

The Bertrand paradox is also in The Pleasures of Probability by Isaac. It’s covered in a non-mathematical way in the book Paradoxes from A to Z by Clark. Edwin Jaynes studied the problem and proposed a solution in a somewhat famous 1973 paper, titled The Well-Posed Problem.

The original problem can be read in French in Bertrand’s work, which is available online here or here (starting at the bottom of page 4).

Code

The MATLAB, R and Python code can be found here. In the code, I have labelled the methods A, B and C instead 1, 2 and 3.

Simulating a Poisson point process on a disk

Sometimes one needs to simulate a Poisson point process on a disk. I know I often do. A disk or disc, depending on your spelling preference, is isotropic or rotationally-invariant, so a lot of my simulations of a Poisson point process happen in a circular simulation window when I am considering such a setting. For example, maybe you want to consider a single wireless receiver in a Poisson network of wireless transmitters, which only cares about the distance to a transmitter. Alternatively, maybe you want to randomly sprinkle a virtual cake. What to do? A Poisson point process on a disk is the answer.

In this post I will simulate a Poisson point process with intensity \(\lambda>0\) on a disk with radius \(r>0\).

Steps

The simulation steps are very similar to those in the previous post where I simulated a  homogeneous Poisson point process on a rectangle, and I suggest going back to that post if you are not familiar with the material. The main difference between simulation on a rectangle and a disk is the positioning of the points, but first we’ll look at the number of points.

Number of points

The number of points of a Poisson point process falling within a circle of radius \(r>0\) is a Poisson random variable with mean  \(\lambda A\), where \(A=\pi r^2\) is the area of the disk. As in the rectangular case, this is the most complicated part of the simulation procedure. But as long as your preferred programming language can produce (pseudo-)random numbers according to a Poisson distribution, you can simulate a homogeneous Poisson point process on a disk.

To do this in MATLAB,  use the poissrnd function with the argument \(\lambda A\). In R, it is done similarly with the standard  function rpois . In Python, we can use either the scipy.stats.poisson or numpy.random.poisson function from the SciPy or NumPy libraries.

Locations of points

We need to position all the points randomly and uniformly on a disk. In the case of the rectangle, we worked in Cartesian coordinates. It is then natural that we now work in polar coordinates.  I’ll denote the angular and radial coordinate respectively by \(\theta\) and \(\rho\). To generate the random angular (or \(\theta\)) values, we simply produce uniform random variables between zero and one, which is what all standard (pseudo-)random number generators do in programming languages. But we then multiply all these numbers by \(2\pi\), meaning that all the numbers now fall between \(0\) and \(2\pi\).

To generate the random radial (or \(\rho\)) values, a reasonable guess would be to do the same as before and generate uniform random variables between zero and one, and then multiply them by the disk radius \(r\). But that would be wrong.

Before multiplying uniform random variables by the radius, we must take the square root of all the random numbers. We then multiply them by the radius, generating random variables between \(0\) and \(r\). (We must take the square root because the area element of a sector or disk is proportional to the radius squared, and not the radius.) These random numbers do not have a uniform distribution, due to the square root, but in fact their distribution is an example of the triangular distribution, which is defined with three real-valued parameters \(a\), \(b\) and \(c\), and for our case, set \(a=0\) and \(b=c=r\).

In summary, if \(U\) and \(V\) are two independent uniform random variables on \((0,1)\), then random point located uniformly on a disk of radius \(r\) has the polar coordinates \((r\sqrt(U), 2\pi V)\).

From polar to Cartesian coordinates

That’s it. We have generated polar coordinates for points randomly and uniformly located in a disk. But to plot the points, often we have to convert coordinates back to Cartesian form. This is easily done in MATLAB with the pol2cart function. In languages without such a function, trigonometry comes to the rescue: \(x=\rho\cos(\theta)\) and \(y=\rho\sin(\theta)\).

Equal x and y axes

Sometimes the plotted points more resemble points on an ellipse than a disk due to the different scaling of the x and y axes. To fix this in MATLAB, run the command: axis square. In Python, set axis(‘equal’) in your plot; see this page for a demonstration.

Code

I’ll now give some code in MATLAB, R and Python, which, as you can see, are all very similar

MATLAB
%Simulation window parameters
r=1; %radius of disk
xx0=0; yy0=0; %centre of disk

areaTotal=pi*r^2; %area of disk
 
%Point process parameters
lambda=100; %intensity (ie mean density) of the Poisson process
 
%Simulate Poisson point process
numbPoints=poissrnd(areaTotal*lambda);%Poisson number of points
theta=2*pi*(rand(numbPoints,1)); %angular coordinates
rho=r*sqrt(rand(numbPoints,1)); %radial coordinates

%Convert from polar to Cartesian coordinates
[xx,yy]=pol2cart(theta,rho); %x/y coordinates of Poisson points

%Shift centre of disk to (xx0,yy0)
xx=xx+xx0;
yy=yy+yy0;
 
%Plotting
scatter(xx,yy);
xlabel('x');ylabel('y');
axis square;
R

Note: it is a bit tricky to write “<-” in the R code (as it automatically changes to the html equivalent in the HTML editor I am using), so I have usually used “=” instead of the usual “<-”.

#Simulation window parameters
r=1; #radius of disk
xx0=0; yy0=0; #centre of disk

areaTotal=pi*r^2; #area of disk

#Point process parameters
lambda=100; #intensity (ie mean density) of the Poisson process

#Simulate Poisson point process
numbPoints=rpois(1,areaTotal*lambda);#Poisson number of points
theta=2*pi*runif(numbPoints);#angular  of Poisson points
rho=r*sqrt(runif(numbPoints));#radial coordinates of Poisson points

#Convert from polar to Cartesian coordinates
xx=rho*cos(theta);
yy=rho*sin(theta);

#Shift centre of disk to (xx0,yy0)
xx=xx+xx0;
yy=yy+yy0;

#Plotting
par(pty="s")
plot(xx,yy,'p',xlab='x',ylab='y',col='blue');

Of course, with the amazing spatial statistics library spatstat, simulating a Poisson point process in R is even easier.

library("spatstat"); #load spatial statistics library
#create Poisson "point pattern" object
ppPoisson=rpoispp(lambda,win=disc(radius=r,centre=c(xx0,yy0))) 
plot(ppPoisson); #Plot point pattern object
#retrieve x/y values from point pattern object
xx=ppPoisson$x; 
yy=ppPoisson$y;

Actually, you can even do it all in two lines: one for loading the spatstat library and one for creating and plotting the point pattern object.

Python

Note: “lambda” is a reserved word in Python (and other languages), so I have used “lambda0” instead.

import numpy as np; #NumPy package for arrays, random number generation, etc
import matplotlib.pyplot as plt #for plotting

#Simulation window parameters
r=1;  #radius of disk
xx0=0; yy0=0; #centre of disk
areaTotal=np.pi*r**2; #area of disk

#Point process parameters
lambda0=100; #intensity (ie mean density) of the Poisson process

#Simulate Poisson point process
numbPoints = np.random.poisson(lambda0*areaTotal);#Poisson number of points
theta=2*np.pi*np.random.uniform(0,1,numbPoints); #angular coordinates 
rho=r*np.sqrt(np.random.uniform(0,1,numbPoints)); #radial coordinates 

#Convert from polar to Cartesian coordinates
xx = rho * np.cos(theta);
yy = rho * np.sin(theta);

#Shift centre of disk to (xx0,yy0) 
xx=xx+xx0; yy=yy+yy0;

#Plotting
plt.scatter(xx,yy, edgecolor='b', facecolor='none', alpha=0.5 );
plt.xlabel("x"); plt.ylabel("y");
plt.axis('equal');
Julia

After writing this post, I later wrote the code in Julia. The code is here and my thoughts about Julia are here.

Results

MATLAB
R 
Python  

Further reading

The third edition of the classic book Stochastic Geometry and its Applications by Chiu, Stoyan, Kendall and Mecke details on page 54 how to uniformly place points on a disk, which they call the radial way. The same simulation section appears in the previous edition by Stoyan, Kendall and Mecke (Chiu didn’t appear as an author until the current edition), though these books in general have little material on simulation methods. There is the book Spatial Point Patterns: Methodology and Applications with R written by spatial statistics experts  Baddeley, Rubak and Turner, which covers the spatial statistics (and point process simulation) R-package spatstat.