Gaussian Archives – H. Paul Keeler

Wiener or Brownian (motion) process

One of the most important stochastic processes is the Wiener process or Brownian (motion) process. In a previous post I gave the definition of a stochastic process (also called a random process) with some examples of this important random object, including random walks. The Wiener process can be considered a continuous version of the simple random walk. This continuous-time stochastic process is a highly studied and used object. It plays a key role different probability fields, particularly those focused on stochastic processes such as stochastic calculus and the theories of Markov processes, martingales, Gaussian processes, and Levy processes.

The Wiener process is named after Norbert Wiener, but it is called the Brownian motion process or often just Brownian motion due to its historical connection as a model for Brownian movement in liquids, a physical phenomenon observed by Robert Brown. But the physical process is not true a Wiener process, which can be treated as an idealized model. I will use the terms Wiener process or Brownian (motion) process to differentiate the stochastic process from the physical phenomenon known as Brownian movement or Brownian process.

The Wiener process is arguably the most important stochastic process. The other important stochastic process is the Poisson (stochastic) process, which I cover in another post. I have written that and the current post with the same structure and style, reflecting and emphasizing the similarities between these two fundamental stochastic process.

In this post I will give a definition of the standard Wiener process. I will also describe some of its key properties and importance. In future posts I will cover the history and generalizations of this stochastic process.

Definition

In the stochastic processes literature there are different definitions of the Wiener process. These depend on the settings such as the level of mathematical rigour. I give a mathematical definition which captures the main characteristics of this stochastic process.

Definition: Standard Wiener or Brownian (motion) process

A real-valued stochastic process $\{W_t:t\geq 0 \}$ defined on a probability space $(\Omega,\mathcal{A},\mathbb{P})$ is a standard Wiener (or Brownian motion) process if it has the following properties:

The initial value of the stochastic process $\{W_t:t\geq 0 \}$ is zero with probability one, meaning $P(W_0=0)=1$.

The increment $W_t-W_s$ is independent of the past, that is, $W_u$, where $0\leq u\leq s$.

The increment $W_t-W_s$ is a normal variable with mean $o$ and variance $t-s$.

In some literature, the initial value of the stochastic process may not be given. Alternatively, it is simply stated as $W_0=0$ instead of the more precise (probabilistic) statement given above.

Also, some definitions of this stochastic process include an extra property or two. For example, from the above definition, we can infer that increments of the standard Wiener process are stationary due to the properties of the normal distribution. But a definition may include something like the following property, which explicitly states that this stochastic process is stationary.

For $0\leq u\leq s$, the increment $W_t-W_s$ is equal in distribution to $W_{t-s}$.

The definitions may also describe the continuity of the realizations of the stochastic process, known as sample paths, which we will cover in the next section.

It’s interesting to compare these defining properties with the corresponding ones of the homogeneous Poisson stochastic process. Both stochastic processes build upon divisible probability distributions. Using this property, Lévy processes generalize these two stochastic processes.

Properties

The definition of the Wiener process means that it has stationary and independent increments. These are arguably the most important properties as they lead to the great tractability of this stochastic process. The increments are normal random variables, implying they can have both positive and negative (real) values.

The Wiener process exhibits closure properties, meaning you apply certain operations, you get another Wiener process. For example, if $W= \{W_t:t\geq 0 \}$ is a Wiener process, then for a scaling constant $c>0$, the resulting stochastic process $\{W_{ct}/\sqrt{c}:t \geq 0 \}$is also a Wiener process. Such properties are useful for proving mathematical results.

Two realizations of a Wiener (or Brownian motion) process. The sample paths are continuous (but non-differentiable) almost everywhere.

Properties such as independence and stationarity of the increments are so-called distributional properties. But the sample paths of this stochastic process are also interesting. A sample path of a Wiener process is continuous almost everywhere. (The term almost everywhere comes from measure theory, but it simply means that the only region where the property does not hold is mathematically negligible.) Despite the continuity of the sample paths, they are nowhere differentiable. (Historically, it was a challenge to find such a function, but a classic example is the Weierstrass function.)

The standard Wiener process has the Markov property, making it an example of a Markov process. The standard Wiener process $W=\{ W_t\}_{t\geq 0}$ is a martingale. Interestingly, the stochastic process $W=\{ W_t^2-t\}_{t\geq 0}$ is also a martingale. The Wiener process is a fundamental object in martingale theory.

There are many other properties of the Brownian motion process; see the Further reading section for, well, further reading.

Importance

Playing a main role in the theory of probability, the Wiener process is considered the most important and studied stochastic process. It has connections to other stochastic processes and is central in stochastic calculus and martingales. Its discovery led to the development to a family of Markov processes known as diffusion processes.

The Wiener process also arises as the mathematical limit of other stochastic processes such as random walks, which is the subject of Donsker’s theorem or invariance principle, also known as the functional central limit theorem.

The Wiener process is a member of some important families of stochastic processes, including Markov processes, Lévy processes, and Gaussian processes. This stochastic process also has many applications. For example, it plays a central role in quantitative finance. It is also used in the physical sciences as well as some branches of social sciences, as a mathematical model for various random phenomena.

Generalizations and modifications

For the Brownian motion process, the index set and state space are respectively the non-negative numbers and real numbers, that is $T=[0,\infty)$ and $S=[0,\infty)$, so it has both continuous index set and state space. Consequently, changing the state space, index set, or both offers an ways for generalizing or modifying the Wiener (stochastic) process.

A single realization of a two-dimensional Wiener (or Brownian motion) process. Each vector component is an independent standard Wiener process.

Simulating

The defining properties of the Wiener process, namely independence and stationarity of increments, results in it being easy to simulate. The Wiener can be simulated provided random variables can be simulated or sampled according to a normal distribution. The main challenge is that the Wiener process is a continuous-time stochastic process, but computer simulations run in a discrete universe.

I will leave the details of sampling this stochastic process for another post.

Simulating a Poisson point process on a n-dimensional sphere

In the previous post I outlined how to simulate or sample a homogeneous Poisson point process on the surface of a sphere. Now I will consider a homogeneous Poisson point process on the $(n-1)-$ sphere, which is the surface of the Euclidean ball in $n$ dimensions.

This is a short post because it immediately builds off the previous post. For positioning the points uniformly, I will use Method 2 from that post, which uses normal random variables, as it immediately gives a fast method in $n$ dimensions.

I wrote this post and the code more for curiosity than any immediate application. But simulating a Poisson point process in this setting requires placing points uniformly on a sphere. And there are applications in that, such as Monte Carlo integration methods, as mentioned in this post, which nicely details different sampling methods.

Steps

As is the case for other shapes, simulating a Poisson point process requires two steps.

Number of points

The number of points of a Poisson point process on the surface of a sphere of radius $r>0$ is a Poisson random variable. The mean of this random variable is $\lambda S_{n-1}$, where $S_{n-1}$ is the surface area of the sphere. For a ball embedded in $n$ dimension, the area of the corresponding sphere is given by

$$S_{n-1} = \frac{2 \pi ^{n/2} }{\Gamma(n/2)} r^{n-1},$$

where $\Gamma$ is the gamma function, which is a natural generalization of the factorial. In MATLAB, we can simply use the function gamma. In Python, we need to use the SciPy function scipy.special. gamma.

Locations of points

For each point on the sphere, we generate $n$ standard normal or Gaussian random variables, say, $W_1, \dots, W_n$, which are independent of each other. These random variables are the Cartesian components of the random point. We rescale the components by the Euclidean norm, then multiply by the radius $r$.

For $i=1,\dots, n$, we obtain

$$X_i=\frac{rW_i}{(W_1^2+\cdots+W_n^2)^{1/2}}.$$

These are the Cartesian coordinates of a point uniformly scattered on a sphere with radius $r$ and a centre at the origin.

How does it work?

In the post on the circle setting, I gave a more detailed outline of the proof, where I said the method is like the Box-Muller transform in reverse. The joint density of the normal random variables is from a multivariate normal distribution with zero correlation. This joint density a function of the Cartesian equation for a sphere. This means the density is constant on the sphere, implying that the angle of the point $(W_1,\dots, W_n)$ will be uniformly distributed.

The vector formed from the normal variables $(W_1,\dots,W_n)$ is a random variable with a chi distribution. But the final vector, which stretches from the origin to the point $(X_1,\dots,X_n)$, has length one, because we rescaled it with the Euclidean norm.

Code

The code for all my posts is located online here. For this post, the code in MATLAB and Python is here.

Simulating a Poisson point process on a sphere

In this post I’ll describe how to simulate or sample a homogeneous Poisson point process on the surface of a sphere. I have already simulated this point process on a rectangle, triangle disk, and circle.

Of course, by sphere, I mean the everyday object that is the surface of a three-dimensional ball, where this two-dimensional object is often denoted by $S^2$. Mathematically, this is a generalization from a Poisson point process on a circle, which is slightly simpler than randomly positioning points on a disk. I recommend reading those two posts first, as a lot of the material presented here builds off them.

I have not needed such a simulation in my own work, but I imagine there are many reasons why you would want to simulate a Poisson point process on a sphere. As some motivation, we can imagine these points on a sphere representing, say, meteorites or lightning hitting the Earth.

The generating the number of points is not difficult. The trick is positioning the points on the sphere in a uniform way. As is often the case, there are various ways to do this, and I recommend this post, which lists the main ones. I will use two methods that I consider the most natural and intuitive ones, namely using spherical coordinates and normal random variables, which is what I did in the post on the circle.

Incidentally, a simple modification allows you to scatter the points uniformly inside the sphere, but you would typically say ball in mathematics, giving a Poisson point process inside a ball; see below for details.

Steps

As always, simulating a Poisson point process requires two steps.

Number of points

The number of points of a Poisson point process on the surface of a sphere of radius $r>0$ is a Poisson random variable with mean $\lambda S_2$, where $S_2=4\pi r^2$ is the surface area of the sphere. (In this post I give some details for simulating or sampling Poisson random variables or, more accurately, variates.)

Locations of points

For any homogeneous Poisson point process, we need to position the points uniformly on the underlying space, which is in this case is the sphere. I will outline two different methods for positioning the points randomly and uniformly on a sphere.

Method 1: Spherical coordinates

The first method is based on spherical coordinates $(\rho, \theta,\phi)$, where the radial coordinate $\rho\geq 0$, and the angular coordinates $0 \leq \theta\leq 2\pi$ and $0\leq \phi \leq \pi$. The change of coordinates gives $x=\rho\sin(\theta)\cos(\phi)$, $y=\rho\sin(\theta)\sin(\phi)$, and $z=\rho\cos(\phi)$.

Now we use Proposition 1.1 in this paper. For each point, we generate two uniform variables $V$ and $\Theta$ on the respective intervals $(-1,1)$ and $(0,2\pi)$. Then we place the point with the Cartesian coordinates

$$X = r \sqrt{1-V^2} \cos\Theta, $$

$$Y = r \sqrt{1-V^2}\sin\Theta, $$

$$ Z=r V. $$

This method places a uniform point on a sphere with a radius $r$.

How does it work?

I’ll skip the precise details, but give some interpretation of this method. The random variable $\Phi := \arccos V$ is the $\phi$-coordinate of the uniform point, which implies $\sin \Phi=\sqrt{1-V^2}$, due to basic trigonometric identities. The area element in polar coordinates is $dA = \rho^2 \sin\phi d\phi d\theta $, which is constant with respect to $\theta$. After integrating with respect to $\phi$, we see that the random variable $V=\cos\Phi$ needs to be uniform (instead of $\Phi$) to ensure the point is uniformly located on the surface.

Method 2: Normal random variables

For each point, we generate three standard normal or Gaussian random variables, say, $W_x$, $W_y$, and $W_z$, which are independent of each other. (The term standard here means the normal random variables have mean $\mu =0$ and standard deviation $\sigma=1$.) The three random variables are the Cartesian components of the random point. We rescale the components by the Euclidean norm, then multiply by the radius $r$, giving

$$X=\frac{rW_x}{(W_x^2+W_y^2+W_z^2)^{1/2}},$$

$$Y=\frac{rW_y}{(W_x^2+W_y^2+W_z^2)^{1/2}},$$

$$Z=\frac{rW_z}{(W_x^2+W_y^2+W_z^2)^{1/2}}.$$

These are the Cartesian coordinates of a point uniformly scattered on a sphere with radius $r$ and a centre at the origin.

How does it work?

The procedure is somewhat like the Box-Muller transform in reverse. In the post on the circle setting, I gave an outline of the proof, which I recommend reading. The joint density of the normal random variables is from a multivariate normal distribution with zero correlation. This joint density is constant on the sphere, implying that the angle of the point $(W_x, W_y, W_z)$ will be uniformly distributed.

The vector formed from the normal variables $(W_x, W_y,W_z)$ is a random variable with a chi distribution. We can see that the vector from the origin to the point $(X,Y,Z)$ has length one, because we rescaled it with the Euclidean norm.

Plotting

Depending on your plotting software, the points may more resemble points on an ellipsoid than a sphere due to the different scaling of the x, y and z axes. To fix this in MATLAB, run the command: axis square. In Python, it’s not straightforward to do this, as it seems to lack an automatic function, so I have skipped it.

Results

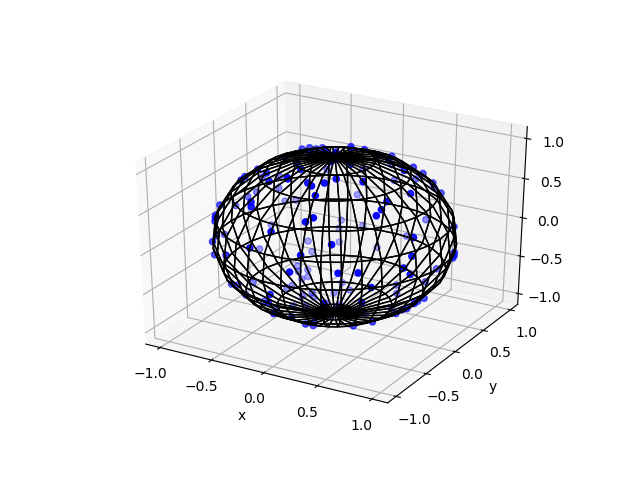
I have presented some results produced by code written in MATLAB and Python. The blue points are the Poisson points on the sphere. I have used a surface plot (with clear faces) to illustrate the underling sphere in black.

MATLAB

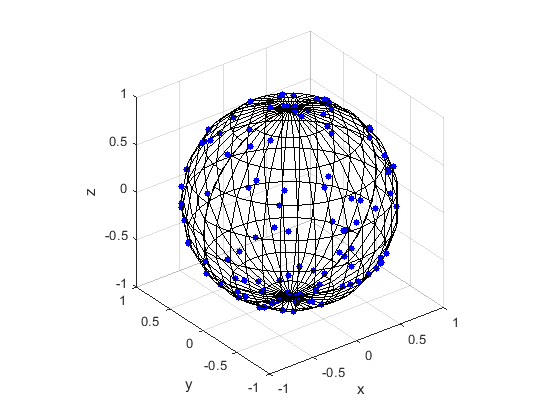
Python

Note: The aspect ratio in 3-D Python plots tends to squash the sphere slightly, but it is a sphere.

Code

The code for all my posts is located online here. For this post, the code in MATLAB and Python is here. In Python I used the library mpl_toolkits for doing 3-D plots.

Poisson point process inside the sphere

Perhaps you want to simulate a Poisson point process inside the ball. There are different ways we can do this, but I will describe just one way, which builds off Method 1 for positioning the points uniformly. (In a later post, I will modify Method 2, giving a way to uniformly position points inside the ball.)

For this simulation method, you need to make two simple modifications to the simulation procedure.

Number of points

The number of points of a Poisson point process inside a sphere of radius $r>0$ is a Poisson random variable with mean $\lambda V_3$, where $V_3=4\pi r^3$ is the volume of the sphere.

Locations of points

We will modify Method 1 as outlined above. To sample the points uniformly in the sphere, you need to generate uniform variables on the unit interval $(0,1)$, take their cubic roots, and then, multiply them by the radius $r$. (This is akin to the step of taking the square root in the disk setting.) The random variables for the angular coordinates are generated as before.

Simulating a Poisson point process on a circle

In this post, I’ll take a break from the more theoretical posts. Instead I’ll describe how to simulate or sample a homogeneous Poisson point process on a circle. I have already simulated this point process on a rectangle, triangle and disk. In some sense, I should have done this simulation method before the disk one, as it’s easier to simulate. I recommend reading that post first, as the material presented here builds off it.

Sampling a homogeneous Poisson point process on a circle is rather straightforward. It just requires using a fixed radius and uniformly choose angles from interval $(0, 2\pi)$. But the circle setting gives an opportunity to employ a different method for positioning points uniformly on circles and, more generally, spheres. This approach uses Gaussian random variables, and it becomes much more efficient when the points are placed on high dimensional spheres.

Steps

Simulating a Poisson point process requires two steps: simulating the random number of points and then randomly positioning each point.

Number of points

The number of points of a Poisson point process on circle of radius $r>0$ is a Poisson random variable with mean $\lambda C$, where $C=2\pi r$ is the circumference of the circle. You just need to be able to need to produce (pseudo-)random numbers according to a Poisson distribution.

To generate Poisson variables in MATLAB, use the poissrnd function with the argument $\lambda C$. In Python, use either the scipy.stats.poisson or numpy.random.poisson function from the SciPy or NumPy libraries. (If you’re curious how Poisson simulation works, I suggest seeing this post for details on sampling Poisson random variables or, more accurately, variates.)

Locations of points

For a homogeneous Poisson point process, we need to uniformly position points on the underlying space, which is this case is a circle. We will look at two different ways to position points uniformly on a circle. The first is arguably the most natural approach.

Method 1: Polar coordinates

We use polar coordinates due to the nature of the problem. To position all the points uniformly on a circle, we simple generate uniform numbers on the unit interval $(0,1)$. We then multiply these random numbers by $2\pi$.

We have generated polar coordinates for points uniformly located on the circle. To plot the points, we have to convert the coordinates back to Cartesian form by using the change of coordinates: $x=\rho\cos(\theta)$ and $y=\rho\sin(\theta)$.

Method 2: Normal random variables

For each point, we generate two standard normal or Gaussian random variables, say, $W_x$ and $W_y$, which are independent of each other. (The term standard here means the normal random variables have mean $\mu =0$ and standard deviation $\sigma=1$.) These two random variables are the Cartesian components of a random point. We then rescale the two values by the Euclidean norm, giving

$$X=\frac{W_x}{(W_x^2+W_y^2)^{1/2}},$$

$$Y=\frac{W_y}{(W_x^2+W_y^2)^{1/2}}.$$

These are the Cartesian coordinates of points uniformly scattered around a unit circle with centre at the origin. We multiply the two random values $X$ and $Y$ by the $r>0$ for a circle with radius $r$.

How does it work?

The procedure is somewhat like the Box-Muller transform in reverse. I’ll give an outline of the proof. The joint density of the random variables $W_x$ and $W_y$ is that of the bivariate normal distribution with zero correlation, meaning it has the joint density

$$ f(x,y)=\frac{1}{2\pi}e^{[-(x^2+y^2)/2]}.$$

We see that the function $f$ is a constant when we trace around any line for which $(x^2+y^2)$ is a constant, which is simply the Cartesian equation for a circle (where the radius is the square root of the aforementioned constant). This means that the angle of the point $(W_x, W_y)$ will be uniformly distributed.

Now we just need to look at the distance of the random point. The vector formed from the pair of normal variables $(W_x, W_y)$ is a Rayleigh random variable. We can see that the vector from the origin to the point $(X,Y)$ has length one, because we rescaled it with the Euclidean norm.

Results

I have presented some results produced by code written in MATLAB and Python. The blue points are the Poisson points on the sphere. I have used a surface plot (with clear faces) in black to illustrate the underling sphere.

MATLAB

Python

Code

The code for all my posts is located online here. For this post, the code in MATLAB and Python is here.