Tag: clustering

Cox point process

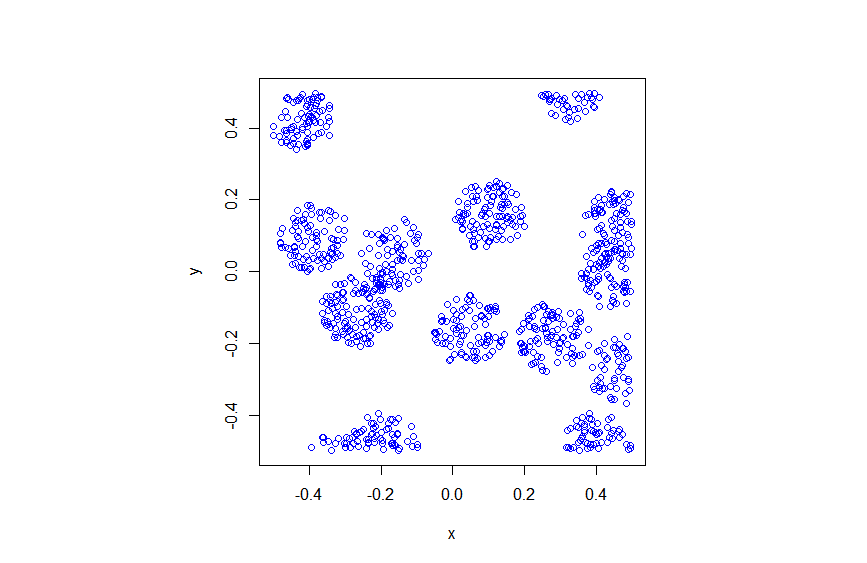
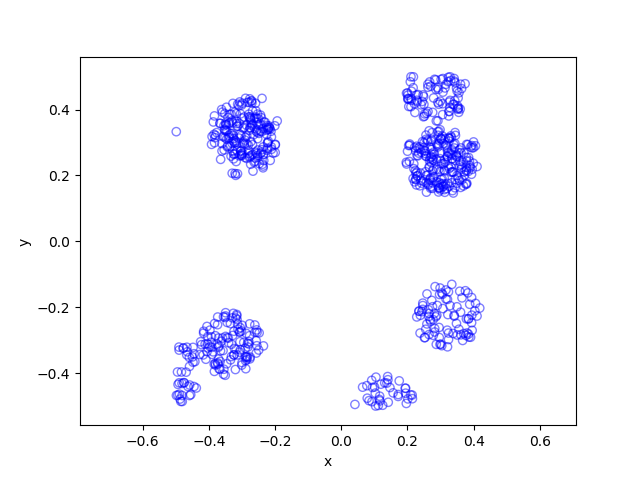
In previous posts I have often stressed the importance of the Poisson point process as a mathematical model. But it can be unsuitable for certain mathematical models.  We can generalize it by first considering a non-negative random measure, called a driving or directing measure. Then a Poisson point process, which is independent of the random driving measure, is generated by using the random measure as its intensity or mean measure. This doubly stochastic construction gives what is called a Cox point process.

In practice we don’t typically observe the driving measure. This means that it’s impossible to distinguish a Cox point process from a Poisson point process if there’s only one realization available. By conditioning on the random driving measure, we can use the properties of the Poisson point process to derive those of the resulting Cox point process.

By the way, Cox point processes are also known as doubly stochastic Poisson point processes. Guttorp and Thorarinsdottir argue that we should call them the Quenouille point processes, as Maurice Quenouille introduced an example of it before Sir David Cox. But I opt for the more common name.

In this post I’ll cover a couple examples of Cox point processes. But first I will need to give a more precise mathematical definition.

Definition

We consider a point process defined on some underlying mathematical space \(\mathbb{S}\), which is sometimes called the carrier space or state space.  The underlying space is often the real line \(\mathbb{R}\), the plane \(\mathbb{R}^2\), or some other familiar mathematical space like a square lattice.

For the first definition, we use the concept of a random measure.

Let \(M\) be a non-negative random measure on \(\mathbb{S} \). Then a point process \(\Phi\) defined on some underlying space \(\mathbb{S}\) is a Cox point process driven by the intensity measure \(M\) if the conditional distribution of \(\Phi\) is a Poisson point process with intensity function \(M\).

We can give a slightly less general definition of a Cox  point process by using a random intensity function.

Let \(Z=\{Z(x):x\in\mathbb{S} \}\) be a non-negative random field such that with probability one, \(x\rightarrow Z(x)\) is a locally integrable function. Then a point process \(\Phi\) defined on some underlying space \(\mathbb{S}\) is a Cox point process driven by \(Z\) if the conditional distribution of \(\Phi\) is a Poisson point process with intensity function \(Z\).

The random driving measure \(M\) is then simply the integral
$$
M(B)=\int_B Z(x)\, dx , \quad B\subseteq S.
$$

Over-dispersion

The random driving measures take different forms, giving different Cox point processes. But there is a general observation that can be made for all Cox point processes. For any region \(B \subseteq S\), it can be shown that the number of points \(\Phi (B)\) adheres to the inequality
$$
\mathbb{Var} [\Phi (B)] \geq \mathbb{E} [\Phi (B)],
$$

where \(\mathbb{Var} [\Phi (B)] \) is the variance of the random variable \(\Phi (B)\).  As a comparison, for a Poisson point process \(\Phi’\), the variance of \(\Phi’ (B)\) is simply \(\mathbb{Var} [\Phi’ (B)] =\mathbb{E} [\Phi’ (B)]\).  Due to its greater variance, the Cox point process is said to be over-dispersed compared to the Poisson point process.

Special cases

There is an virtually unlimited number of ways to define a random driving measure, where each one yields a different a Cox point process. But in general we are restricted by examining only tractable and interesting Cox point processes. I will give some common examples, but I stress that the Cox point process family is very large.

Mixed Poisson point process

For the random driving measure \(M\), an obvious example is the product form \(M= Y \mu \), where \(Y\) is some independent non-negative random variable and \(\mu\) is the Lebesgue measure on \(\mathbb{S}\). This driving measure gives the mixed Poisson point process. The random variable \(Y\) is the only source of randomness.

Log-Gaussian Cox point process

Instead of a random variable, we can use a non-negative random field to define a random driving measure.  We then have the product \(M= Y \mu \), where \(Y\) is now some independent non-negative random field. (A random field is a collection of random variables indexed by some set, which in this case is the underlying space \(\mathbb{S}\).)

Arguably the most tractable and used random field is the Gaussian random field. This random field, like Gaussian or normal random variables, takes both negative and positive values. But if we define the random field such that its logarithm is a Gaussian field \(Z\), then we obtain the non-negative random driving measure \(M=\mu e^Z \), giving the log-Gaussian Cox point process.

This point process has found applications in spatial statistics.

Cox-Poisson line-point process

To construct this Cox point process, we first consider a Poisson line process, which I discussed previously.  Given a Poisson line process, we then place an independent one-dimensional Poisson point process on each line. We then obtain an example of a Cox point process, which we could call a Cox line-point process or a Cox-Poisson line-point process. (But I am not sure of the best name.)

Researchers have recently used this point process to study wireless communication networks in cities, where the streets correspond to Poisson lines. For example, see these two preprints:

  1. Continuum percolation for Cox point processes
  2. Poisson Cox Point Processes for Vehicular Networks

Shot-noise Cox point process

We construct the next Cox point process by first considering a Poisson point process on the space \(\mathbb{S}\) to create a shot noise term. (Shot noise is just the sum of some function over all the points of a point process.) We then use it as the driving measure of the Cox point process.

More specifically, we first introduce a kernel function \(k(\cdot,\cdot)\) on \(\mathbb{S}\), where \(k(x,\cdot)\) is a probability density function for all points \(x\in \mathbb{S}\). We then consider a Poisson point process \(\Phi’\) on \(\mathbb{S}\times (0,\infty)\). We assume the Poisson point process \(\Phi’\) has a locally integrable intensity function \(\mu \).

(We can interpret the point process \(\Phi’\) as a spatially-dependent marked Poisson point process, where the unmarked Poisson point process is defined on \(\mathbb{S}\). We then assume each point \(X\) of this unmarked point process has a mark \(T \in (0,\infty)\) with probability density \(\mu(X,t)\).)

The resulting shot noise

$$
Z(x)= \sum_{(Y,T)\in \Phi’} T \, k(Y,x)\,,
$$

gives the random field. We then use it as the random intensity function to drive the shot-noise Cox point process.

In previous posts, I have detailed how to simulate non-Poisson point processes such as the Matérn and Thomas cluster point processes. These are examples of a Neyman-Scott point process, which is a special case of a shot noise Cox point process. All these point processes find applications in spatial statistics.

Simulation

Unfortunately, there is no universal way to simulate all Cox point processes. (And even if there were one, it would not be the most optimal way for every Cox point process.) The simulation method depends on how the Cox point process is constructed, which usually means how its directing or driving measure is defined.

In previous posts I have presented ways (with code) to simulate these Cox point processes:

In addition to the Matérn and Thomas point processes, there are ways to simulate more general shot noise Cox point processes. I will cover that in another post.

Further reading

For general Cox point processes, I suggest: Chapter 6 in the monograph Poisson Processes by Kingman; Chapter 5 in Statistical Inference and Simulation for Spatial Point Processes by Møller and Waagepetersen; and Section 5.2 in Stochastic Geometry and its Applications by Chiu, Stoyan, Kendall and Mecke. For a much more mathematical treatment, see Chapter 13 in Lectures on the Poisson Process by Last and Penrose. Grandell wrote two detailed monographs titled Mixed Poisson Process and Doubly Stochastic Poisson Processes.

Motivated by applications in spatial statistics, Jesper Møller has (co)-written papers on specific Cox point processes. For example:

  • 2001, Møller, Syversveen, and Waagepetersen, Log Gaussian Cox Processes;
  • 2003, Møller, Shot noise Cox Processes;
  • 2005, Møller and Torrisi,Generalised shot noise Cox processes.

I also suggest the survey article:

  • 2003, Møller and Waagepetersen, Modern statistics for spatial point processes.

Beyond the Poisson point process

As great as the Poisson point process is — and it is pretty great — it is sadly not always suitable for mathematical models. The tractability of this point process is due to the independence of the locations of its points. Informally, this means that point locations of  a Poisson point process in any region will not affect the probability of finding other points in some other region. But such independence may not be true or even approximately true when trying to develop a mathematical model for certain phenomena.

Clustering and Repulsion

One can quickly think of examples where the Poisson point process is not a suitable model. For example, if a star is part of a galaxy, then it is more likely that another star will be located nearby. Conversely, given the location of a tree in the forest, then usually it is less likely to then find another tree relatively nearby, because trees need a certain amount of land to draw water from the earth.  In the language of point processes, we say that the stars tend to show clustering, while the trees tend to show repulsion.

To better model phenomena like like trees and stars, we can use point processes that also exhibit the properties of clustering and repulsion. In fact, a good part of spatial statistics has been dedicated to developing statistical tools for testing if repulsion or clustering exists in observed point patterns, which is the spatial statistics term used for samples of objects that can be represented as points in space. (A point process is a random object, so a single realization or outcome of a point process is an example of a point pattern.)

The Poisson point process lies halfway between these two categories, meaning that its points show an equal degree of clustering and repulsion. Mathematically, this can be made more formal by, for example, using something called factorial moment measures, which are mathematical objects used to study point processes.

For probability applications, Błaszczyszyn and Yogeshwaran developed a framework using factorial moment measures, which allowed them to classify point process into what they called super-Poisson and sub-Poisson, referring respectively to point processes with points that tend to cluster and repel more.

Point Process Operations

If a Poisson point processes is not suitable for certain models, then we need to develop and use other point processes that exhibit clustering or repulsion. Fortunately, one way to develop such point processes is to apply certain point process operations to Poisson and point processes in general. For developing new point processes, researchers have largely studied three types types of point process operations: thinning, superposition, and clustering. (But there are other operations one can apply to a point process such as randomly moving the points.)

Thinning

To apply the thinning operation means to use some rule for selectively removing points from a point process \(\Phi\) to form a new point process \(\Phi_p\). A rule may be purely random such as the rule known as \(p\)-thinning. For this rule, each point of \(\Phi\) is independently removed (or kept) with some probability \(p\) (or \(1-p\)). This thinning method can be likened to looking at each point, flipping a biased coin with probability \(p\) for heads, and removing the point if a head occurs.

This rule may be generalized by introducing a non-negative function \(p(x)\leq 1\), where \(x\) is a point in the space on which the point process is defined.  This allows us to define a location-dependent \(p(x)\)-thinning, where now the probability of a point being removed is \(p(x)\) and is dependent on where the point \(x\) of \(\Phi\) is located on the underlying space.

The thinning operation is very useful, and I will write more about it in another post, including some examples implemented in code.

Superposition

The superposition of two or more point processes simply means taking the union of two or more point processes. (Point processes can be considered as random sets, which is why point process notation consists of notation from set theory, as well as other mathematical branches.)

More formally, if there is a countable collection of point processes \(\Phi_1,\Phi_2\dots\), then their superposition
\[
\Phi=\bigcup_{i=1}^{\infty}\Phi_i,
\]
also forms a point process. If the point processes are all independent and Poisson, then the superposition will be another Poisson point process, meaning we have not produced a new point process.

Clustering

Related to superposition is a point operation known as clustering, which entails replacing every point \(x\) in a given point process \(\Phi\) with a cluster of points \(N^x\). Each cluster is also a point process, but with a finite number of points. The union of all the clusters forms a cluster point process,  that is
\[
\Phi_c=\bigcup_{x\in \Phi}N^x.
\]

In two previous blogs I have already used this point process operation to construct the Matérn and Thomas (cluster) point processes, which both involve using an underlying Poisson point process. Each point of this point process was assigned a Poisson random number of points, and then the points were uniformly scattered on a disk (for Matérn) or scattered according to a two-dimensional normal distribution (for Thomas). They are members of a family of point processes called Neyman-Scott point processes.

Clustering or repulsion?

I mentioned earlier that in spatial statistics there are statistical tools for testing if clustering or repulsion exists in observed point patterns, usually by comparing it to the Poisson point process, which often serves as a benchmark. For example, in spatial statistics the second factorial moment measure is used for the descriptive statistic called Ripley’s \(K\)-function and its rescaled version, Ripley’s \(L\)-function. Keeping with the alphabetical theme, another example of such a statistic is the \(J\)-function, which was introduced by Van Lieshout and Baddeley.

Further reading

For spatial statistics in general, I always recommend the book Spatial Point Patterns: Methodology and Applications with R written by spatial statistics experts Baddeley, Rubak and Turner, which covers the spatial statistics (and point process simulation) R-package spatstat. This book covers statistically testing point patterns to see if they exhibit more clustering or repulsion, with details for the relevant functions in  spatstat.  For an introduction on factorial moment framework by Błaszczyszyn and Yogeshwaran for clustering and repulsion comparison, see this chapter from a published collection of of lecture notes.

In Chapter 5 of the classic text Stochastic Geometry and its Applications by Chiu, Stoyan, Kendall and Meck, the point process operations thinning are described and used to construct new point processes.  The similar material is covered in the previous edition by Stoyan, Kendall and Mecke.

On a more theoretical level, operations of point processes are covered in the second volume of An Introduction to the Theory of Point Processes by Daley and Vere-Jones. (These convergence results are now a little dated, because there are now various convergence results for point processes based on Stein’s method, which are not included in the book.)

See the previous posts for details and citations on the  Matérn and Thomas (cluster) point processes.

Simulating a Thomas cluster point process

Sometimes with just a little tweaking of a point process, you can get a new  point process. An example of this is the Thomas point process, which is a type of cluster point process, meaning that its randomly located points tend to form random clusters.  This point process is an example of a family of cluster point processes known as Neyman-Scott point processes, which have been used as models in spatial statistics and telecommunications. If that sounds familiar, that is because this point process is very similar to the Matérn point cluster process, which I covered in the previous post. 

The only difference between the two point processes is how the points are randomly located. In each cluster of a Thomas point process, each individual point is located according to two independent zero-mean normal variables with variance \(\sigma^2\), describing the \(x\) and \(y\) coordinates relative to the cluster centre, whereas each point of a Matérn point process is located uniformly in a disk.

Working in polar coordinates, an equivalent way to simulate a Thomas point process is to use independent and identically-distributed Rayleigh random variables for the radial (or \(\rho\)) coordinates, instead of using random variables with a triangular distribution, which are used to simulate the Matérn point process. This method works because in polar coordinates a uniform random variable for the angular (or \(\theta\) ) coordinate and a Rayleigh random variable for the angular (or \(\rho\)) is equivalent to in Cartesian coordinates two independent zero-mean normal variables. This is exactly the trick behind the Box-Muller transform for generating normal random variables using just uniform random variables.

If you’re familiar with simulating the Matérn point process, the most difference is what size to make the simulation window for the parents points. I cover that in the next section.  

Overview

Simulating a Thomas cluster point process requires first simulating a homogeneous Poisson point process with intensity \(\lambda>0\) on some simulation window, such as a rectangle, which is the simulation window I will use here. Then for each point of this underlying point process, simulate a Poisson number of points with mean \(\mu>0\), and for each point simulate two independent zero-mean normal variables with variance \(\sigma^2\), corresponding to the (relative) Cartesian coordinates .

The underlying  point process is sometimes called the parent (point) process, and its points are centres of the cluster disks. The subsequent point process on all the disks is called daughter (point) process and it forms the clusters. I have already written about simulating the homogeneous Poisson point processes on a rectangle and a disk, so  those posts are good starting points, and I will not focus  too much on details for these steps steps.

Importantly, like the Matérn point process, it’s possible for daughter points to appear in the simulation window that come from parents points outside the simulation window. To handle these edge effects, the point processes must be first simulated on an extended version of the simulation window. Then only the daughter points within the simulation window are kept and the rest are removed.  

We can add a strip of some width \(d\) all around the simulation window. But what value does \(d\) take? Well, in theory, it is possible that a daughter point comes from a parent point that is very far from the simulation window. But that probability becomes vanishingly small as the distance increases, due to the daughter points being located according to zero-mean normal random variables. 

For example, if a single parent is at a distance \(d=6 \sigma\) from the simulation, then there is about a $1/1 000 000 000$ chance that a single daughter point will land in the simulation window. The probability is simply \(1-\Phi(6 \sigma)\), where \(\Phi\) is the cumulative distribution function of a normal variable with zero mean and standard deviation \(\sigma>0\).  This is what they call a six sigma event.  In my code, I set \(d=6 \sigma\), but \(d=4 \sigma\) is good enough, which is the value that the R library spatstat uses by default.  

Due to this approximation, this simulation cannot be called a perfect simulation, despite the approximation being highly accurate. In practice, it will not have no measurable effect on simulation results, as the number of simulations will rarely be high enough for (hypothetical) daughter points to come from (hypothetical) parent points outside the window. 

Steps

Number of points

Simulate the underlying or parent Poisson point process on the rectangle with \(N_P\) points. Then for each point, simulate a Poisson number of points, where each disk now has \(D_i\) number of points. Then the total number of points is simply \(N=D_1+\dots +D_{P}=\sum_{i=1}^{N_P}D_i \). The random variables \(P\) and \(D_i\) are Poisson random variables with respective means \(\lambda A\) and \(\mu\), where \(A\) is the area of the rectangular simulation window. To simulate these random variables in MATLAB, use the poissrnd function. To do this in R, use the  standard function rpois. In Python, we can use either functions scipy.stats.poisson or numpy.random.poisson from the SciPy or NumPy libraries.

Locations of points

The points of the parent point process are randomly positioned by using Cartesian coordinates. For a homogeneous Poisson point process, the \(x\) and \(y\) coordinates of each point are independent uniform points, which is also the case for the binomial point process, covered in an earlier post.

As mentioned in the introduction of this post, the points of all the daughter point process are randomly positioned by either using polar  coordinates or Cartesian coordinates, due to the Box-Muller transform. But because we ultimately convert back to Cartesian coordinates (for example, to plot the points), we will work entirely in this coordinate system.  Each point is then simply positioned with two independent zero-mean normal random variables, representing the \(x\) and \(y\) coordinates relative to the original parent point.

Shifting all the points in each cluster disk

In practice (that is, in the code), all the daughter points are simulated relative to the origin. Then for each cluster disk, all the points need to be shifted, so the origin coincides with the parent point, which completes the simulation step.

To use vectorization in the code,  the coordinates of each cluster point are repeated by the number of daughters in the corresponding cluster by using the functions repelem in MATLAB, rep in R, and repeat in Python. 

Code

I have implemented the simulation procedure in MATLAB, R and Python, which as usual are all very similar. The code can be downloaded here.

MATLAB
 %Simulation window parameters xMin=-.5; xMax=.5; yMin=-.5; yMax=.5; %Parameters for the parent and daughter point processes lambdaParent=10;%density of parent Poisson point process lambdaDautgher=100;%mean number of points in each cluster sigma=0.05;%sigma for normal variables (ie random locations) of daughters %Extended simulation windows parameters rExt=7*sigma; %extension parameter -- use factor of deviation %for rExt, use factor of deviation sigma eg 6 or 7 xMinExt=xMin-rExt; xMaxExt=xMax+rExt; yMinExt=yMin-rExt; yMaxExt=yMax+rExt; %rectangle dimensions xDeltaExt=xMaxExt-xMinExt; yDeltaExt=yMaxExt-yMinExt; areaTotalExt=xDeltaExt*yDeltaExt; %area of extended rectangle %Simulate Poisson point process for the parents numbPointsParent=poissrnd(areaTotalExt*lambdaParent,1,1);%Poisson number %x and y coordinates of Poisson points for the parent xxParent=xMinExt+xDeltaExt*rand(numbPointsParent,1); yyParent=yMinExt+yDeltaExt*rand(numbPointsParent,1); %Simulate Poisson point process for the daughters (ie final poiint process) numbPointsDaughter=poissrnd(lambdaDautgher,numbPointsParent,1); numbPoints=sum(numbPointsDaughter); %total number of points %Generate the (relative) locations in Cartesian coordinates by %simulating independent normal variables xx0=normrnd(0,sigma,numbPoints,1); yy0=normrnd(0,sigma,numbPoints,1); %replicate parent points (ie centres of disks/clusters) xx=repelem(xxParent,numbPointsDaughter); yy=repelem(yyParent,numbPointsDaughter); %translate points (ie parents points are the centres of cluster disks) xx=xx(:)+xx0; yy=yy(:)+yy0; %thin points if outside the simulation window booleInside=((xx>=xMin)&(xx<=xMax)&(yy>=yMin)&(yy<=yMax)); %retain points inside simulation window xx=xx(booleInside); yy=yy(booleInside); %Plotting scatter(xx,yy);
R

Note: it is a bit tricky to write “<-” in the R code (as it automatically changes to the html equivalent in the HTML editor I am using), so I have usually used “=” instead of the usual “<-”.

 #Simulation window parameters xMin=-.5; xMax=.5; yMin=-.5; yMax=.5; #Parameters for the parent and daughter point processes lambdaParent=10;#density of parent Poisson point process lambdaDaughter=100;#mean number of points in each cluster sigma=0.05; #sigma for normal variables (ie random locations) of daughters #Extended simulation windows parameters rExt=7*sigma; #extension parameter #for rExt, use factor of deviation sigma eg 6 or 7 xMinExt=xMin-rExt; xMaxExt=xMax+rExt; yMinExt=yMin-rExt; yMaxExt=yMax+rExt; #rectangle dimensions xDeltaExt=xMaxExt-xMinExt; yDeltaExt=yMaxExt-yMinExt; areaTotalExt=xDeltaExt*yDeltaExt; #area of extended rectangle #Simulate Poisson point process for the parents numbPointsParent=rpois(1,areaTotalExt*lambdaParent);#Poisson number of points #x and y coordinates of Poisson points for the parent xxParent=xMinExt+xDeltaExt*runif(numbPointsParent); yyParent=yMinExt+yDeltaExt*runif(numbPointsParent); #Simulate Poisson point process for the daughters (ie final poiint process) numbPointsDaughter=rpois(numbPointsParent,lambdaDaughter); numbPoints=sum(numbPointsDaughter); #total number of points #Generate the (relative) locations in Cartesian coordinates by #simulating independent normal variables xx0=rnorm(numbPoints,0,sigma); yy0=rnorm(numbPoints,0,sigma); #replicate parent points (ie centres of disks/clusters) xx=rep(xxParent,numbPointsDaughter); yy=rep(yyParent,numbPointsDaughter); #translate points (ie parents points are the centres of cluster disks) xx=xx+xx0; yy=yy+yy0; #thin points if outside the simulation window booleInside=((xx&amp;amp;amp;amp;amp;gt;=xMin)&amp;amp;amp;amp;amp;amp;(xx&amp;amp;amp;amp;amp;lt;=xMax)&amp;amp;amp;amp;amp;amp;(yy&amp;amp;amp;amp;amp;gt;=yMin)&amp;amp;amp;amp;amp;amp;(yy&amp;amp;amp;amp;amp;lt;=yMax)); #retain points inside simulation window xx=xx[booleInside]; yy=yy[booleInside]; #Plotting par(pty="s") plot(xx,yy,'p',xlab='x',ylab='y',col='blue');

Of course, as I have mentioned before, simulating a spatial point processes in R is even easier with the powerful spatial statistics library spatstat. The Thomas cluster point process is simulated by using the function rThomas, but other cluster point processes, including Neyman-Scott types, are possible.

Python

Note: in previous posts I used the SciPy functions for random number generation, but now use the NumPy ones, but there is little difference, as SciPy builds off NumPy.

 import numpy as np;&amp;amp;amp;amp;amp;nbsp; # NumPy package for arrays, random number generation, etc import matplotlib.pyplot as plt&amp;amp;amp;amp;amp;nbsp; # For plotting # Simulation window parameters xMin = -.5; xMax = .5; yMin = -.5; yMax = .5; # Parameters for the parent and daughter point processes lambdaParent = 10; # density of parent Poisson point process lambdaDaughter = 100; # mean number of points in each cluster sigma = 0.05; # sigma for normal variables (ie random locations) of daughters #Extended simulation windows parameters rExt=7*sigma; #extension parameter #for rExt, use factor of deviation sigma eg 6 or 7 xMinExt = xMin - rExt; xMaxExt = xMax + rExt; yMinExt = yMin - rExt; yMaxExt = yMax + rExt; # rectangle dimensions xDeltaExt = xMaxExt - xMinExt; yDeltaExt = yMaxExt - yMinExt; areaTotalExt = xDeltaExt * yDeltaExt; # area of extended rectangle # Simulate Poisson point process for the parents numbPointsParent = np.random.poisson(areaTotalExt * lambdaParent);# Poisson number of points # x and y coordinates of Poisson points for the parent xxParent = xMinExt + xDeltaExt * np.random.uniform(0, 1, numbPointsParent); yyParent = yMinExt + yDeltaExt * np.random.uniform(0, 1, numbPointsParent); # Simulate Poisson point process for the daughters (ie final poiint process) numbPointsDaughter = np.random.poisson(lambdaDaughter, numbPointsParent); numbPoints = sum(numbPointsDaughter); # total number of points # Generate the (relative) locations in Cartesian coordinates by # simulating independent normal variables xx0 = np.random.normal(0, sigma, numbPoints); # (relative) x coordinaets yy0 = np.random.normal(0, sigma, numbPoints); # (relative) y coordinates # replicate parent points (ie centres of disks/clusters) xx = np.repeat(xxParent, numbPointsDaughter); yy = np.repeat(yyParent, numbPointsDaughter); # translate points (ie parents points are the centres of cluster disks) xx = xx + xx0; yy = yy + yy0; # thin points if outside the simulation window booleInside=((xx&amp;amp;amp;amp;amp;gt;=xMin)&amp;amp;amp;amp;amp;amp;(xx&amp;amp;amp;amp;amp;lt;=xMax)&amp;amp;amp;amp;amp;amp;(yy&amp;amp;amp;amp;amp;gt;=yMin)&amp;amp;amp;amp;amp;amp;(yy&amp;amp;amp;amp;amp;lt;=yMax)); # retain points inside simulation window xx = xx[booleInside]; yy = yy[booleInside]; # Plotting plt.scatter(xx, yy, edgecolor='b', facecolor='none', alpha=0.5); plt.xlabel("x"); plt.ylabel("y"); plt.axis('equal');
Julia 

After writing this post, I later wrote the code in Julia. The code is here and my thoughts about Julia are here.

Results

The results show that the clusters of Thomas point process tend to be more blurred than those of Matérn point process, which has cluster edges clearly defined by the disks.  The points of of a Thomas point process can be far away from the centre of each cluster, depending on the variance of the normal random variables used in the simulation. 

MATLAB

R

Python

Further reading

Thomas (and Matérn) cluster point processes and more generally Neyman-Scott point processes are covered in standard books on the related fields of spatial statistics, point processes and stochastic geometry, such as the following: Spatial Point Patterns: Methodology and Applications with R by  Baddeley, Rubak and Turner, on page 461; Statistical Analysis and Modelling of Spatial Point Patterns Statistics by Illian, Penttinen, Stoyan, amd Stoyan, page 370 and Section 6.3.2; Stochastic Geometry and its Applications by Chiu, Stoyan, Kendall and Mecke,  on page 173; and; Statistical Inference and Simulation for Spatial Point Processes by Møller and Waagepetersen, in Section 5.3. I would probably recommend the first two books for beginners. 

The Thomas point process has also appeared in models of wireless networks, which we covered in the book Stochastic Geometry Analysis of Cellular Networks by Błaszczyszyn, Haenggi, Keeler, and Mukherjee, Section 8.1.8.

More generally, Neyman-Scott point processes belong to a family of point processes called shot noise Cox point processes; see the paper by Møller. 

I mentioned above the book Spatial Point Patterns: Methodology and Applications with R , which is written by spatial statistics experts Baddeley, Rubak and Turner. It covers the spatial statistics (and point process simulation) R-package spatstat.

In my travels on the web, I found this post where the writer also simulates the Thomas and Matérn point processes in Python, independent of my code.  That code is a bit different to mine because I use the repeat function and simulate all the Poisson variables at once, instead of using a for-loop and simulating a Poisson variable for each iteration.  I also think it’s not quite correct because I do not see how they account for edge effects.  

Simulating a Matérn cluster point process

A Matérn cluster point process is a type of cluster point process, meaning that its randomly located points tend to form random clusters. (I skip the details here, but by using techniques from spatial statistics, it is possible to make the definition of clustering more precise.) This point process is an example of a family of cluster point processes known as Neyman-Scott point processes, which have been used in spatial statistics and telecommunications.

I should point out that the Matérn cluster point process should not be confused with the Matérn hard-core point process, which is a completely different type of point process. (For a research article, I have actually written code in MATLAB that simulates this type of point process.) Bertril Matérn proposed at least four types of point processes, and his name also refers to a specific type of covariance function used to define Gaussian processes.

Overview

Simulating a Matérn cluster point process requires first simulating  a homogeneous Poisson point process with an intensity \(\lambda>0\) on some simulation window, such as a rectangle, which is the simulation window I will use here. Then for each point of this underlying point process, simulate a Poisson number of points with mean \(\mu>0\) uniformly on a disk with a constant radius \(r>0\). The underlying  point process is sometimes called the parent (point) process, and its points are centres of the cluster disks.

The subsequent point process on all the disks is called daughter (point) process and it forms the clusters. I have already written about simulating the homogeneous Poisson point processes on a rectangle and a disk, so those posts are good starting points, and I will not focus  too much on details for these steps.

Edge effects

The main challenge behind sampling this point process, which I originally forgot about in an earlier version of this post, is that it’s possible for daughter points to appear in the simulation window that come from parents points outside the simulation window. In other words, parents points outside the simulation window contribute to points inside the window.

To remove these edge effects, the point processes must be simulated on an extended version of the simulation window. Then only the daughter points within the simulation window are kept and the rest are removed.  Consequently, the points are simulated on an extended window, but we only see the points inside the simulation window.

To create the extended simulation window, we can add a strip of width \(r\) all around the simulation window. Why? Well, the distance \(r\) is the maximum distance from the simulation window that a possibly contributing parent point (outside the simulation window) can exist, while still having daughter points inside the simulation window. This means it is impossible for a hypothetical parent point beyond this distance (outside the extended window) to generate a daughter point that can fall inside the simulation window. 

Steps

Number of points

Simulate the underlying or parent Poisson point process on the rectangle with \(N_P\) points. Then for each point, simulate a Poisson number of points, where each disk now has \(D_i\) number of points. Then the total number of points is simply \(N=D_1+\dots +D_{P}=\sum_{i=1}^{N_P}D_i \). The random variables \(P\) and \(D_i\) are Poisson random variables with respective means \(\lambda A\) and \(\mu\), where \(A\) is the area of the rectangular simulation window. To simulate these random variables in MATLAB, use the poissrnd function. To do this in R, use the  standard function rpois. In Python, we can use either functions scipy.stats.poisson or numpy.random.poisson from the SciPy or NumPy libraries.

Locations of points

The points of the parent point process are randomly positioned by using Cartesian coordinates. For a homogeneous Poisson point process, the \(x\) and \(y\) coordinates of each point are independent uniform points, which is also the case for the binomial point process, covered in a previous post. The points of all the daughter point process are randomly positioned by using polar  coordinates. For a homogeneous Poisson point process, the \(\theta\) and \(\rho\) coordinates of each point are independent  variables,  respectively with uniform and triangle distributions, which was covered in a previous post. Then we  convert coordinates back to Cartesian form, which is easily done in MATLAB with the pol2cart function. In languages without such a function: \(x=\rho\cos(\theta)\) and \(y=\rho\sin(\theta)\).

Shifting all the points in each cluster disk

In practice (that is, in the code), all the daughter points are simulated in a disk with its centre at the origin. Then for each cluster disk, all the points have to be shifted to the origin is the center of the cluster, which completes the simulation step.

To use vectorization in the code,  the coordinates of each cluster point are repeated by the number of daughters in the corresponding cluster by using the functions repelem in MATLAB, rep in R, and repeat in Python. 

Code

I’ll now give some code in MATLAB, R and Python, which you can see are all very similar. It’s also located here.

MATLAB

The MATLAB code is located here.

R

The R code is located here.

Of course, as I have mentioned before, simulating a spatial point processes in R is even easier with the powerful spatial statistics library spatstat. The Matérn cluster point process is simulated by using the function rMatClust, but other cluster point processes, including Neyman-Scott types, are possible.

Python

The Pyhon code is located here.

Note: in previous posts I used the SciPy functions for random number generation, but now use the NumPy ones, but there is little difference, as SciPy builds off NumPy.

Julia 

After writing this post, I later wrote the code in Julia. The code is here and my thoughts about Julia are here.

Results

MATLAB

R

Python  

Further reading

Matérn cluster point processes and more generally Neyman-Scott point processes are covered in standard books on the related fields of spatial statistics, point processes and stochastic geometry, such as the following: Spatial Point Patterns: Methodology and Applications with R by  Baddeley, Rubak and Turner, on page 461; Statistical Analysis and Modelling of Spatial Point Patterns Statistics by Illian, Penttinen, Stoyan, amd Stoyan, Section 6.3.2, starting on page 370; Stochastic Geometry and its Applications by Chiu, Stoyan, Kendall and Mecke,  on page 173; and; Statistical Inference and Simulation for Spatial Point Processes by Moller and Waagepetersen, in Section 5.3. I would probably recommend the first two books for beginners.

The Matérn point process has also appeared in models of wireless networks, which we covered in the book Stochastic Geometry Analysis of Cellular Networks by Błaszczyszyn, Haenggi, Keeler, and Mukherjee, Section 8.1.8.

I mentioned above the book Spatial Point Patterns: Methodology and Applications with R , which is written by spatial statistics experts Baddeley, Rubak and Turner. It covers the spatial statistics (and point process simulation) R-package spatstat.