H. Paul Keeler

New Link – math3ma.com

In my internet wanderings, I stumbled upon this blog:

The writer, Tae-Danae Bradley, wrote a PhD applying category theory (a field of mathematics that strives for abstraction) to problems in machine learning.

New link: gregorygundersen.com

I came across this blog:

http://gregorygundersen.com/blog

The writer now focuses mostly on financial models and techniques, but earlier posts cover topics in probability and statistics.

I found myself recently wondering who the first author was of a seminal paper that created a mathematical field. I did some online digging and I noted my findings here for others who may ask the same question.

Percolation theory

The 1957 paper by S.R. Broadbent and J.M. Hammersley gave birth to percolation theory. I noticed the author affiliations:

S.R. Broadbent, United Glass Bottle Manufacturers
J.M. Hammersley, United Kingdom Atomic Energy Research Establishment Harwell

I knew John Hammersley’s name already, as he had co-written a classic book on Monte Carlo methods. Indeed, if you look at the end of the paper, you see the paper’s idea was born at an early conference on Monte Carlo methods.

But who was S.R. Broadbent? And what was he doing at a bottle factory?

Probability work

This Broadbent character was a bit mysterious. At first, it seemed as though the writer always published as S.R. Broadbent — so much so, I thought he might be a she. Such things have happened before, as the story behind the influential 1960 paper by A.H. Land and A.G. Doig demonstrated.¹

From the start I could see S.R. Broadbent was strong in probability. In the 1950s Broadbent wrote probability papers, including a 1953 paper co-written by the British father of stochastic geometry David G. Kendall. ² The Broadbent and Kendall paper has the improbable title The Random Walk of Trichostrongylus retortaeformis. (It’s a type of larva.)

And then I was thrown by the title of a paper co-written by Broadbent in the 1960s: A computer assessment of media schedules.

Simon says ley lines are just spatial coincidences

Then I lost track of S.R. Broadbent in terms of academic papers. I had almost given up, assuming Broadbent had left academia. But then I saw Broadbent’s name mentioned in the acknowledgements in a famous spatial statistics paper written by David Kendall in 1989. In the paper Kendalls cites a 1980 paper written by S.R. Broadbent. The subject was the statistics of ley lines — it’s a thing — showing they can be explained by mere chance. And in the acknowledgements Kendall thanks a certain Simon Broadbent — presumably he’s S.R. Broadbent whose paper Kendall cited.

Had I found the S.R. Broadbent? I was a bit skeptical, but then he’s mentioned as Simon Broadbent in this obituary of Hammersley:

Despite the title of the paper, ‘Poor man’s Monte Carlo’, the lasting contributions are the clear statement of the problem of counting self-avoiding walks, the use of subadditivity to prove the existence of the connective constant, and the discussion of random media that culminated in Simon Broadbent’s formulation of the percolation model.

That reassured me.

And then I found two 1950s papers (1954 and 1958) by a Simon Broadbent, not S.R. Broadbent, published in the Journal of the Royal Statistical Society Series C: Applied Statistics. I had actually stumbled upon the 1958 paper earlier in my searches. Initially I didn’t think it was S.R. Broadbent because the journal referred to the author as Dr Simon Broadbent, and I thought only medical doctors do that to each other. But it’s a statistics journal. So it’s probably S.R. Broadbent. Also, for this 1954 paper in the same journal they call him Mr Simon Broadbent.

And then I looked at the paper by Broadbent that David Kendall cited, and in that paper Broadbent acknowledges Kendall. And then I noticed that this paper was actually written by Simon Broadbent, but Kendall had cited the paper and written its author as S.R. Broadbent. The final link. S.R. Broadbent was Simon Broadbent — whoever that was.

I thought I had come to the end. But I hadn’t.

Advertising guru

A non-scientific article had floated up in my search results talking about the death of some big name in advertising. Seeing the title and reading the start, I thought it couldn’t be the same Simon Broadbent.

Simon asked simple questions: How does advertising work? How much advertising is enough? How can we tell whether our ad campaign has succeeded? Is adspend profitable?
When he entered advertising in the 60s, none of these questions had satisfactory answers. Many doubted they could ever be answered. Simon did more than anyone to show that advertising can contribute to profit, and that it is not a cost that can be cut with no effect on sales.

But after reading more, I realized this had to be the very same Broadbent.

He answered advertising questions with the rigour of a mathematician and the clarity of a poet. He read engineering at Cambridge, took an applauded first in mathematics and a diploma in statistics at Magdalen, Oxford, and completed his doctorate in statistics at Imperial, London. His poetry was published by Blackwell’s while he was still an undergraduate.

His lifelong interest was applying statistics to problems that nobody had thought amenable to statistical analysis. His paper to the Royal Statistical Society, In Search of the Ley Hunter, debunked claims for the existence of megalithic ley lines, pointing out that there were fewer alleged lines than would be expected from a random distribution of points between which lines could be drawn. Preparing the paper also allowed him to crawl about in Greenwich Park, testing the likely accuracy of stone-age surveying devices using instruments he had built himself.

Simon R. Broadbent made quite the impression in advertising, even being called a global legend in media research. Some of his contributions to this field are mentioned in this published tribute. It seems this field remembered him better than his original field. I couldn’t find any tributes focusing on his mathematical contributions.

Mystery solved, except for what the R stands for.

Back to percolation

Now knowing the S stood for Simon, I noticed that Simon Broadbent is mentioned in the Wikipedia article on percolation theory. The article cites a tutorial article by John Hammersley and Dominic Welsh, which gives the original motivation of percolation theory:

The study of percolation originated from a question posed to one of us by S. R. Broadbent (see Hammersley and Morton 1954). Broadbent was at that time working at the British Coal Utilization Research Association on the design of gas masks for use in coal mines. These masks contained porous carbon granules (the medium) into which gas (the fluid) could penetrate. The pores in a granule constituted a random network of tiny interconnecting tunnels, into which the gas could move by surface adsorption; and the question was what properties of such a random network would assist or inhibit the uptake of gas. If the pores were large enough and richly enough connected, the gas could permeate the interior of a granule; but if the pores were too small or inadequately connected, the gas could not get beyond the outer surface of a granule. Thus there was a critical point, above which the mask worked well and below which it was ineffective. Critical phenomena of this sort are typical of percolation processes, and do not, normally arise in ordinary diffusion.

The original Broadbent and Hammersley paper did mention that Broadbent had previously worked at British Coal Utilisation Research Association (BCURA).

(Another aside, the same Wikipedia article says Rosalind Franklin, whose X-ray work helped reveal the structure of DNA, also worked on porous material at the British Coal Utilisation Research Association, before leaving in 1946, which I guess was before Broadbent started working there. You can read about her career, for example, here.)

Summary

Simon R. Broadbent was a trained engineer and mathematician who co-founded the thriving mathematical discipline of percolation theory, before leaving that world to go revolutionize the field of advertising by using quantitative methods and writing influential books.

New Link – almostsuremath.com

This probability blog came up in my news feed:

https://almostsuremath.com/

It seems to focus on stochastic processes such as Brownian motion and friends.

A Fields Medal goes to another percolation researcher

The Fields Medal is a prize in mathematics awarded every four years to two to four outstanding researchers (forty years old or younger) working in mathematics. One of the medals this year was awarded to French mathematician Hugo Duminil-Copin who has solved problems and obtained new results in the percolation theory which lies in the intersection of probability and statistical physics. Here’s a good Quanta article on Duminil-Copin and some of his work.

(The other winners are June Huh, James Maynard, and Maryna Viazovska.)

The Fields Medal people has been kind to probability researchers in recent years. Previous winners working in probability have included Wendelin Werner (2006), Stanislav Smirov (2010), and Martin Hairer (2014), while other winners in recent years have also made contributions to probability.

All in all, that’s not too shabby for a discipline that for a long, long time wasn’t considered part of mathematics. (That story deserves a post on its own.)

I work nowhere near Duminil-Copin, but I have used some percolation theory in my work. I will write a couple of posts on percolation theory. Eventually, I may even mention some recent work that my collaborators and I have been working on.

New link: xianblog.wordpress.com

I have come across posts on this blog at least three or four times:

https://xianblog.wordpress.com/

It happens, I later discovered, to be maintained by Christian P. Robert, a senior research figure in Markov chain Monte Carlo methods and Bayesian statistics.

New link: extremelearning.com.au

When researching topics for my work (and for posts), I sometimes stumble upon the same blog more than once for different reasons. One of these is this one:

http://extremelearning.com.au/

It’s run by a Tasmanian physicist turned data scientist. Topics include quasi-random sequences, the Fisher-Yates sampling algorithm, and sampling points uniformly on a triangle.

Update: A post on the multi-arm bandit problem, which is a prototypical problem in reinforcement learning.

Poisson (stochastic) process

One of the most important stochastic processes is Poisson stochastic process, often called simply the Poisson process. In a previous post I gave the definition of a stochastic process (also called a random process) alongside some examples of this important random object, including counting processes. The Poisson (stochastic) process is a counting process. This continuous-time stochastic process is a highly studied and used object. It plays a key role in different probability fields, particularly those focused on stochastic processes such as stochastic calculus (with jumps) and the theories of Markov processes, queueing, point processes (on the real line), and Levy processes.

The points in time when a Poisson stochastic process increases form a Poisson point process on the real line. In this setting the stochastic process and the point process can be considered two interpretations of the same random object. The Poisson point process is often just called the Poisson process, but a Poisson point process can be defined on more generals spaces. In some literature, such as the theory of Lévy processes, a Poisson point process is called a Poisson random measure, differentiating the Poisson point process from the Poisson stochastic process. Due to the connection with the Poisson distribution, the two mathematical objects are named after Simeon Poisson, but he never studied these random objects.

The other important stochastic process is the Wiener process or Brownian (motion process), which I cover in another post. The Wiener process is arguably the most important stochastic process. I have written that post and the current one with the same structure and style, reflecting and emphasizing the similarities between these two fundamental stochastic process.

In this post I will give a definition of the homogenous Poisson process. I will also describe some of its key properties and importance. In future posts I will cover the history and generalizations of this stochastic process.

Definition

In the stochastic processes literature there are different definitions of the Poisson process. These depend on the settings such as the level of mathematical rigour. I give a mathematical definition which captures the main characteristics of this stochastic process.

Definition: Homogeneous Poisson (stochastic) process

An integer-valued stochastic process $\{N_t:t\geq 0 \}$ defined on a probability space $(\Omega,\mathcal{A},\mathbb{P})$ is a homogeneous Poisson (stochastic) process if it has the following properties:

The initial value of the stochastic process $\{N_t:t\geq 0 \}$ is zero with probability one, meaning $P(N_0=0)=1$.

The increment $N_t-N_s$ is independent of the past, that is, $N_u$, where $0\leq u\leq s$.

The increment $N_t-N_s$ is a Poisson variable with mean $\lambda (t-s)$.

In some literature, the initial value of the stochastic process may not be given. Alternatively, it is simply stated as $N_0=0$ instead of the more precise (probabilistic) statement given above.

Also, some definitions of this stochastic process include an extra property or two. For example, from the above definition, we can infer that increments of the homogeneous Poisson process are stationary due to the properties of the Poisson distribution. But a definition may include something like the following property, which explicitly states that this stochastic process is stationary.

For $0\leq u\leq s$, the increment $N_t-N_s$ is equal in distribution to $N_{t-s}$.

The definitions may also describe the continuity of the realizations of the stochastic process, known as sample paths, which we will cover in the next section.

It’s interesting to compare these defining properties with the corresponding ones of the standard Wiener stochastic process. Both stochastic processes build upon divisible probability distributions. Using this property, Lévy processes generalize these two stochastic processes.

Properties

The definition of the Poisson (stochastic) process means that it has stationary and independent increments. These are arguably the most important properties as they lead to the great tractability of this stochastic process. The increments are Poisson random variables, implying they can have only positive (integer) values.

The Poisson (stochastic) process exhibits closure properties, meaning you apply certain operations, you get another Poisson (stochastic) process. For example, if we sum two independent Poisson processes $X= \{X_t:t\geq 0 \}$ and $Y= \{Y_t:t\geq 0 \}$, then the resulting stochastic process $Z=Z+Y = \{N_t:t\geq 0 \}$ is also a Poisson (stochastic) process. Such properties are useful for proving mathematical results.

A single realization of a (homogeneous) Poisson stochastic process, where the blue marks show where the process jumps to the next value. In any finite time interval, there are a finite number of jumps.

Properties such as independence and stationarity of the increments are so-called distributional properties. But the sample paths of this stochastic process are also interesting. A sample path of a Poisson stochastic process is almost surely non-decreasing, being constant except for jumps of size one. (The term almost surely comes from measure theory, but it means with probability one.) There are only finitely number of jumps in each finite time interval.

The homogeneous Poisson (stochastic) process has the Markov property, making it an example of a Markov process. The homogenous Poisson process $N=\{ N_t\}_{t\geq 0}$s not a martingale. But interestingly, the stochastic process is $\{ W_t – \lambda t\}_{t\geq 0}$ is a martingale. (Such relations have been used to study such stochastic processes with tools from martingale theory.)

Stochastic or point process?

The Poisson (stochastic) process is a discrete-valued stochastic process in continuous time. The relation these types of stochastic processes and point process is a subtle one. For example, David Cox and Valerie Isham write on page 3 of their monograph:

The borderline between point processes and a number of other kinds of stochastic process is not sharply defined. In particular, any stochastic process in continuous time in which the sample paths are step functions, and therefore any any process with a discrete state space, is associated with a point process, where a point is a time of transition or, more generally, a time of entry into a pre-assigned state or set of states. Whether it is useful to look at a particular process in this way depends on the purpose of the analysis.

For the Poisson case, this association is presented in the diagram below. We can see the Poisson point process (in red) associated with the Poisson (stochastic) process (in blue) by simply looking at the time points where jumps occur.

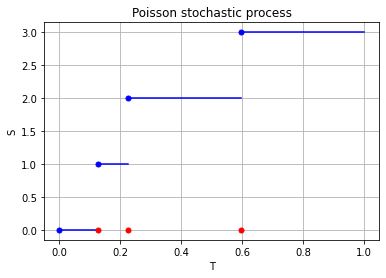
A single realization of a (homogeneous) Poisson stochastic process (in blue). The jumps of the process form a (homogeneous) Poisson point process (in red) on the real line representing time.

Importance

Playing a prominent role in the theory of probability, the Poisson (stochastic) process is a highly important and studied stochastic process. It has connections to other stochastic processes and is central in queueing theory and random measures.

The Poisson process is a building block for more complex continuous-time Markov processes with discrete state spaces, which are used as mathematical models. It is also essential in the study of jump processes and subordinators.

The Poisson (stochastic) process is a member of some important families of stochastic processes, including Markov processes, Lévy processes, and birth-death processes. This stochastic process also has many applications. For example, it plays a central role in quantitative finance. It is also used in the physical sciences as well as some branches of social sciences, as a mathematical model for various random phenomena.

Generalizations and modifications

For the Poisson (stochastic) process, the index set and state space are respectively the non-negative numbers and counting numbers, that is $T=[0,\infty)$ and $S=0, 1, \dots$, so it has a continuous index set but a discrete state space. Consequently, changing the state space, index set, or both offers an ways for generalizing and modifying the Poisson (stochastic) process.

Simulation

The defining properties of the Poisson stochastic process, namely independence and stationarity of increments, results in it being easy to simulate. The Poisson stochastic process can be simulated provided random variables can be simulated or sampled according to a Poisson distributions, which I have covered in this and this post.

Simulating a Poisson stochastic process is similar to simulating a Poisson point process. (Basically, it is the same method in a one-dimensional setting.) But I will leave the details of sampling this stochastic process for another post.

Wiener or Brownian (motion) process

One of the most important stochastic processes is the Wiener process or Brownian (motion) process. In a previous post I gave the definition of a stochastic process (also called a random process) with some examples of this important random object, including random walks. The Wiener process can be considered a continuous version of the simple random walk. This continuous-time stochastic process is a highly studied and used object. It plays a key role different probability fields, particularly those focused on stochastic processes such as stochastic calculus and the theories of Markov processes, martingales, Gaussian processes, and Levy processes.

The Wiener process is named after Norbert Wiener, but it is called the Brownian motion process or often just Brownian motion due to its historical connection as a model for Brownian movement in liquids, a physical phenomenon observed by Robert Brown. But the physical process is not true a Wiener process, which can be treated as an idealized model. I will use the terms Wiener process or Brownian (motion) process to differentiate the stochastic process from the physical phenomenon known as Brownian movement or Brownian process.

The Wiener process is arguably the most important stochastic process. The other important stochastic process is the Poisson (stochastic) process, which I cover in another post. I have written that and the current post with the same structure and style, reflecting and emphasizing the similarities between these two fundamental stochastic process.

In this post I will give a definition of the standard Wiener process. I will also describe some of its key properties and importance. In future posts I will cover the history and generalizations of this stochastic process.

Definition

In the stochastic processes literature there are different definitions of the Wiener process. These depend on the settings such as the level of mathematical rigour. I give a mathematical definition which captures the main characteristics of this stochastic process.

Definition: Standard Wiener or Brownian (motion) process

A real-valued stochastic process $\{W_t:t\geq 0 \}$ defined on a probability space $(\Omega,\mathcal{A},\mathbb{P})$ is a standard Wiener (or Brownian motion) process if it has the following properties:

The initial value of the stochastic process $\{W_t:t\geq 0 \}$ is zero with probability one, meaning $P(W_0=0)=1$.

The increment $W_t-W_s$ is independent of the past, that is, $W_u$, where $0\leq u\leq s$.

The increment $W_t-W_s$ is a normal variable with mean $o$ and variance $t-s$.

In some literature, the initial value of the stochastic process may not be given. Alternatively, it is simply stated as $W_0=0$ instead of the more precise (probabilistic) statement given above.

Also, some definitions of this stochastic process include an extra property or two. For example, from the above definition, we can infer that increments of the standard Wiener process are stationary due to the properties of the normal distribution. But a definition may include something like the following property, which explicitly states that this stochastic process is stationary.

For $0\leq u\leq s$, the increment $W_t-W_s$ is equal in distribution to $W_{t-s}$.

The definitions may also describe the continuity of the realizations of the stochastic process, known as sample paths, which we will cover in the next section.

It’s interesting to compare these defining properties with the corresponding ones of the homogeneous Poisson stochastic process. Both stochastic processes build upon divisible probability distributions. Using this property, Lévy processes generalize these two stochastic processes.

Properties

The definition of the Wiener process means that it has stationary and independent increments. These are arguably the most important properties as they lead to the great tractability of this stochastic process. The increments are normal random variables, implying they can have both positive and negative (real) values.

The Wiener process exhibits closure properties, meaning you apply certain operations, you get another Wiener process. For example, if $W= \{W_t:t\geq 0 \}$ is a Wiener process, then for a scaling constant $c>0$, the resulting stochastic process $\{W_{ct}/\sqrt{c}:t \geq 0 \}$is also a Wiener process. Such properties are useful for proving mathematical results.

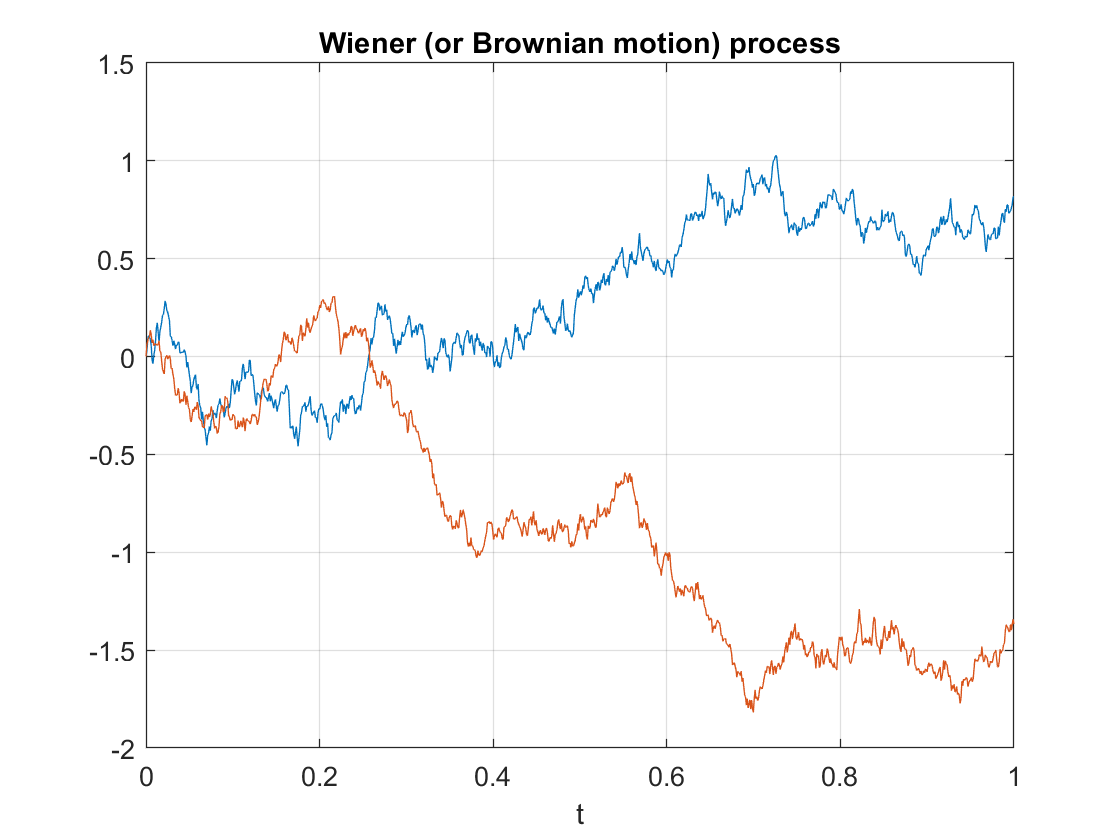
Two realizations of a Wiener (or Brownian motion) process. The sample paths are continuous (but non-differentiable) almost everywhere.

Properties such as independence and stationarity of the increments are so-called distributional properties. But the sample paths of this stochastic process are also interesting. A sample path of a Wiener process is continuous almost everywhere. (The term almost everywhere comes from measure theory, but it simply means that the only region where the property does not hold is mathematically negligible.) Despite the continuity of the sample paths, they are nowhere differentiable. (Historically, it was a challenge to find such a function, but a classic example is the Weierstrass function.)

The standard Wiener process has the Markov property, making it an example of a Markov process. The standard Wiener process $W=\{ W_t\}_{t\geq 0}$ is a martingale. Interestingly, the stochastic process $W=\{ W_t^2-t\}_{t\geq 0}$ is also a martingale. The Wiener process is a fundamental object in martingale theory.

There are many other properties of the Brownian motion process; see the Further reading section for, well, further reading.

Importance

Playing a main role in the theory of probability, the Wiener process is considered the most important and studied stochastic process. It has connections to other stochastic processes and is central in stochastic calculus and martingales. Its discovery led to the development to a family of Markov processes known as diffusion processes.

The Wiener process also arises as the mathematical limit of other stochastic processes such as random walks, which is the subject of Donsker’s theorem or invariance principle, also known as the functional central limit theorem.

The Wiener process is a member of some important families of stochastic processes, including Markov processes, Lévy processes, and Gaussian processes. This stochastic process also has many applications. For example, it plays a central role in quantitative finance. It is also used in the physical sciences as well as some branches of social sciences, as a mathematical model for various random phenomena.

Generalizations and modifications

For the Brownian motion process, the index set and state space are respectively the non-negative numbers and real numbers, that is $T=[0,\infty)$ and $S=[0,\infty)$, so it has both continuous index set and state space. Consequently, changing the state space, index set, or both offers an ways for generalizing or modifying the Wiener (stochastic) process.

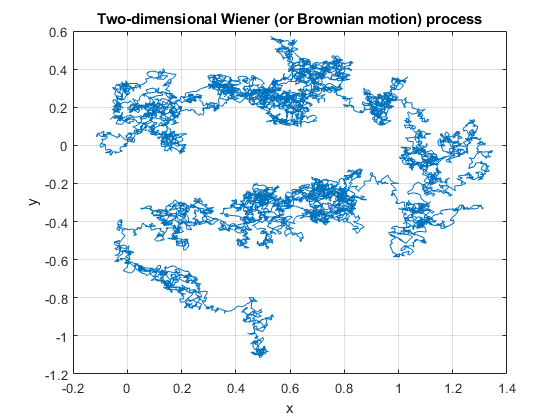
A single realization of a two-dimensional Wiener (or Brownian motion) process. Each vector component is an independent standard Wiener process.

Simulating

The defining properties of the Wiener process, namely independence and stationarity of increments, results in it being easy to simulate. The Wiener can be simulated provided random variables can be simulated or sampled according to a normal distribution. The main challenge is that the Wiener process is a continuous-time stochastic process, but computer simulations run in a discrete universe.

I will leave the details of sampling this stochastic process for another post.

Stochastic processes

I have written a few posts about point processes, which are mathematical objects that seek to represent points randomly scattered over some space. Arguably a much more popular random object is something called a stochastic process. This type of mathematical object, also frequently called a random process, is studied in mathematics. But the origins of stochastic processes stem from various phenomena in the real world.

Stochastic processes find applications representing some type of seemingly random change of a system (usually with respect to time). Examples include the growth of some population, the emission of radioactive particles, or the movements of financial markets. There are many types of stochastic processes with applications in various fields outside of mathematics, including the physical sciences, social sciences, finance, and engineering.

In this post I will cover the standard definition of a stochastic process. But first a quick reminder of some probability basics.

Probability basics

Random experiment

The mathematical field of probability arose from trying to understand games of chance. In these games, some random experiment is performed. A coin is flipped. A die is cast. A card is drawn. These random experiments give the initial intuition behind probability. Such experiments can be considered in more general or abstract terms.

A random experiment has the properties:

Sample space: A sample space, denoted here by $\Omega$, is the set of all (conceptually) possible outcomes of the random experiment;
Outcomes: An outcome, denoted here by $\omega$, is an element of the sample space $\Omega$, meaning $\omega \in \Omega$, and it is called a sample point or realization.
Events: An event is a subset of the sample space $\Omega$ for which probability is defined.

Examples

One die

Consider the rolling a traditional six-sided die with the sides numbered from $1$ to $6$. Its sample space is $\Omega=\{1, 2, 3,4,5,6\}$. A possible event is an even number, corresponding to the outcomes $\{2\}$, $\{4\}$, and $\{6\}$.

Two coins

Consider the flipping two identical coins, where each coin has a head appearing on one side and a tail on the other. We denote the head and tail respectively by $H$ and $T$. Then the sample space $\Omega$ is all the possible outcomes, meaning $\Omega=\{HH, TT, HT, TH\}$. A possible event is at least one head appearing, which corresponds to the outcomes $\{HH\}$, $\{HT\}$, and $\{TH\}$.

Conversely, three heads $\{HHH\}$, the number $5$, or the queen of diamonds appearing are clearly not possible outcomes of flipping two coins, which means they are not elements of the sample space.

Modern probability approach

For a random experiment, we formalize what events are possible (or not) with a mathematical object called a $\sigma$-algebra. (It is also called $\sigma$-field.) This object is a mathematical set with certain properties with respect to set operations. It is a fundamental concept in measure theory, which is the standard approach for the theory of integrals. Measure theory serves as the foundation of modern probability theory.

In modern probability theory, if we want to define a random mathematical object, such as a random variable, we start with a random experiment in the context of a probability space or probability triple $(\Omega,\mathcal{A},\mathbb{P})$, where:

$\Omega$ is a sample space, which is the set of all (conceptually) possible outcomes;
$\mathcal{A}$ is a $\sigma$-algebra or $\sigma$-field, which is a family of events (subsets of $\Omega$);
$\mathbb{P}$ is a probability measure, which assigns probability to each event in $\mathcal{A}$.

To give some intuition behind this approach, David Williams says to imagine that Tyche, Goddess of Chance, chooses a point $\omega\in\Omega$ at random according to the law $\mathbb{P}$ such that an event $A\in \mathcal{A}$ has a probability given by $\mathbb{P}(A)$, where we understand probability with our own intuition. We can also choose $\omega\in\Omega$ by using some physical experiment, as long as it is random.

With this formalism, mathematicians define random objects by using a certain measurable function or mapping that maps to a suitable space of mathematical objects. For example, a real-valued random variable is a measurable function from $\Omega$ to the real line. To consider other random mathematical objects, we just need to define a measurable mapping from $\Omega$ to a suitable mathematical space.

Definition

Stochastic process

Mathematically, a stochastic process is usually defined as a collection of random variables indexed by some set, often representing time. (Other interpretations exists such as a stochastic process being a random function.)

More formally, a stochastic process is defined as a collection of random variables defined on a common probability space $(\Omega,{\cal A}, \mathbb{P} )$, where $\Omega$ is a sample space, ${\cal A}$ is a $\sigma$-algebra, and $\mathbb{P}$ is a probability measure, and the random variables, indexed by some set $T$, all take values in the same mathematical space $S$, which must be measurable with respect to some $\sigma$-algebra $\Sigma$.

Put another way, for a given probability space $( \mathbb{P}, {\cal A}, \Omega)$ and a measurable space $(S, \Sigma)$, a stochastic process is a collection of $S$-valued random variables, which we can write as:

$$\{X(t):t\in T \}.$$

For each $t\in T$, $X(t)$ is a random variable. Historically, a point $t\in T$ was interpreted as time, so $X(t)$ is random variable representing a value observed at time $t$.

Often the collection of random variables $\{X(t):t\in T \}$ is denoted by simply a single letter such as $X$. There are different notations for stochastic processes. For example, a stochastic process can also be written as $\{X(t,\omega):t\in T \}$, reflecting that is function of the two variables, $t\in T$ and $\omega\in \Omega$.

Index set

The set $T$ is called the index set or parameter set of the stochastic process. Typically this set is some subset of the real line, such as the natural numbers or an interval. If the set is countable, such as the natural numbers, then it is a discrete-time stochastic process. Conversely, an interval for the index set gives a continuous-time stochastic process.

(If the index set is some two or higher dimensional Euclidean space or manifold, then typically the resulting stochastic or random process is called a random field.)

State space

The mathematical space $S$ is called the state space of the stochastic process. The precise mathematical space can be any one of many different mathematical sets such as the integers, the real line, $n$-dimensional Euclidean space, the complex plane, or more abstract mathematical spaces. The different spaces reflects the different values that the stochastic process can take.

Sample function

A single outcome of a stochastic process is called a sample function, a sample path, or, a realization. It is formed by taking a single value of each random variable of the stochastic process. More precisely, if $\{X(t,\omega):t\in T \}$ is a stochastic process, then for any point $\omega\in\Omega$, the mapping
\[
X(\cdot,\omega): T \rightarrow S,
\]
is a sample function of the stochastic process $\{X(t,\omega):t\in T \}$. Other names exist such as trajectory, and path function.

Examples

The range of stochastic processes is limitless, as stochastic processes can be used to construct new ones. Broadly speaking, stochastic processes can be classified by their index set and their state space. For example, we can consider a discrete-time and continuous-time stochastic processes.

There are some commonly used stochastic processes. I’ll give the details of a couple of very simple ones.

Bernoulli process

A very simple stochastic process is the Bernoulli process, which is a sequence of independent and identically distributed (iid) random variables. The value of each random variable can be one of two values, typically $0$ and $1$, but they could be also $-1$ and $+1$ or $H$ and $T$. To generate this stochastic process, each random variable takes one value, say, $1$ with probability $p$ or the other value, say, $0$ with probability $1-p$.

We can can liken this stochastic process to flipping a coin, where the probability of a head is $p$ and its value is $1$, while the value of a tail is $0$. In other words, a Bernoulli process is a sequence of iid Bernoulli random variables. The Bernoulli process has the counting numbers (that is, the positive integers) as its index set, meaning $T=1,\dots$, while in this example the state space is simply $S=\{0,1\}$.

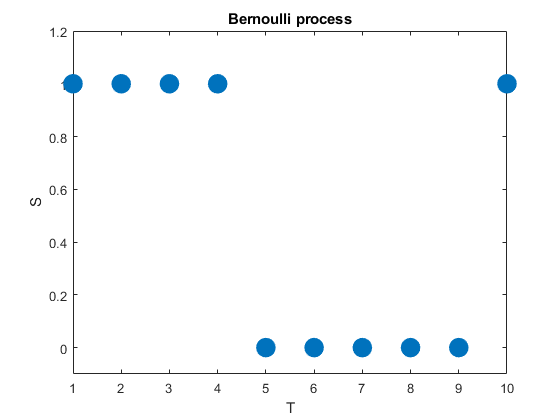
A single realization of a Bernoulli process, one of the simplest stochastic processes. This discrete-time stochastic process only takes two values such as 0 and 1.

(We can easily generalize the Bernoulli process by having a sequence of iid variables with the same probability space.)

Random walks

A random walk is a type of stochastic process that is usually defined as sum of a sequence of iid random variables or random vectors in Euclidean space. Given random walks are formed from a sum, they are stochastic processes that evolve in discrete time. (But some also use the term to refer to stochastic processes that change in continuous time.)

A classic example of this stochastic process is the simple random walk, which is based on a Bernoulli process, where each iid Bernoulli variable takes either the value positive one or negative one. More specifically, the simple random walk increases by one with probability, say, $p$, or decreases by one with probability $1-p$. The index set of this stochastic process is the natural numbers, while its state space is the integers.

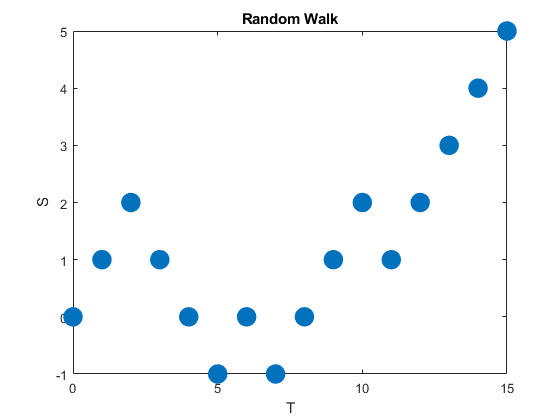
A single realization of a simple (symmetric) random walk. This discrete-time stochastic process is a fundamental object in the history of probability theory.

Random walks can be defined in more general settings such as $n$- dimensional Euclidean space. There are other types of random walks, defined on different mathematical objects, such as lattices and groups, and in general they are highly studied and have many applications in different disciplines.

Markov processes

One important way for classifying stochastic processes is the stochastic dependence between random variables. For the Bernoulli process, there was no dependence between any random variable, giving a very simple stochastic process. But this is not a very interesting stochastic process.

A more interesting (and typically useful) stochastic process is one in which the random variables depend on each other in some way. For example, the next position of a random walk depends on the current position, which in turn depends on the previous position.

A large family of stochastic processes in which the next value depends on the current value are called Markov processes or Markov chains. (Both names are used. The term Markov chain is largely used when either the state space or index is discrete, but there does not seem to be an agreed upon convention. When I think Markov chain, I think discrete time.) The definition of a Markov process has a property that constrains the dependence between the random variables, as the next random variable only depends on the current random variable, and not all the previous random variables. This constraint on the dependence typically renders Markov processes more tractable than general stochastic processes.

It would be difficult to overstate the importance of Markov processes. Their study and application appear throughout probability, science, and technology.

Counting processes

A counting process is a stochastic process that takes the values of non-negative integers, meaning its state space is the counting numbers, and is non-decreasing. A simple example of a counting process is an asymmetric random walk, which increases by one with some probability $p$ or remains the same value with probability $1-p$. In other words, the accumulative sum of a Bernoulli process. This is an example of a discrete-time counting process, but continuous-time ones also exist.

A counting process can be also interpreted as a counting as a random counting measure on the index set.

Two important stochastic processes

The most two important stochastic processes are the Poisson process and the Wiener process (often called Brownian motion process or just Brownian motion). They are important for both applications and theoretical reasons, playing fundamental roles in the theory of stochastic processes. In future posts I’ll cover both the Wiener process and the Poisson process.

Code

The code used to create the plots in this post is found here on my code repository. The code exists in both MATLAB and Python.