Tag: probability space

Stochastic processes

I have written a few posts about point processes, which are mathematical objects that seek to represent points randomly scattered over some space. Arguably a much more popular random object is something called a stochastic process. This type of mathematical object, also frequently called a random process, is studied in mathematics. But the origins of stochastic processes stem from various phenomena in the real world.

Stochastic processes find applications representing some type of seemingly random change of a system (usually with respect to time). Examples include the growth of some population, the emission of radioactive particles, or the movements of financial markets. There are many types of stochastic processes with applications in various fields outside of mathematics, including the physical sciences, social sciences, finance, and engineering.

In this post I will cover the standard definition of a stochastic process. But first a quick reminder of some probability basics.

Probability basics

Random experiment

The mathematical field of probability arose from trying to understand games of chance. In these games, some random experiment is performed. A coin is flipped. A die is cast. A card is drawn. These random experiments give the initial intuition behind probability. Such experiments can be considered in more general or abstract terms.

A random experiment has the properties:

  1. Sample space: A sample space, denoted here by \(\Omega\), is the set of all (conceptually) possible outcomes of the random experiment;
  2. Outcomes: An outcome, denoted here by \(\omega\), is an element of the sample space \(\Omega\), meaning \(\omega \in \Omega\), and it is called a sample point or realization.
  3. Events: An event is a subset of the sample space \(\Omega\) for which probability is defined.
Examples
One die

Consider the rolling a traditional six-sided die with the sides numbered from \(1\) to \(6\). Its sample space is \(\Omega=\{1, 2, 3,4,5,6\}\). A possible event is an even number, corresponding to the outcomes \(\{2\}\), \(\{4\}\), and \(\{6\}\).

Two coins

Consider the flipping two identical coins, where each coin has a head appearing on one side and a tail on the other. We denote the head and tail respectively by \(H\) and \(T\). Then the sample space \(\Omega\) is all the possible outcomes, meaning \(\Omega=\{HH, TT, HT, TH\}\). A possible event is at least one head appearing, which corresponds to the outcomes \(\{HH\}\), \(\{HT\}\), and \(\{TH\}\).

Conversely, three heads \(\{HHH\}\), the number \(5\), or the queen of diamonds appearing are clearly not possible outcomes of flipping two coins, which means they are not elements of the sample space.

Modern probability approach

For a random experiment, we formalize what events are possible (or not) with a mathematical object called a \(\sigma\)-algebra. (It is also called \(\sigma\)-field.) This object is a mathematical set with certain properties with respect to set operations. It is a fundamental concept in measure theory, which is the standard approach for the theory of integrals. Measure theory serves as the foundation of modern probability theory.

In modern probability theory, if we want to define a random mathematical object, such as a random variable, we start with a random experiment in the context of a probability space or probability triple \((\Omega,\mathcal{A},\mathbb{P})\), where:

  1. \(\Omega\) is a sample space, which is the set of all (conceptually) possible outcomes;
  2. \(\mathcal{A}\) is a \(\sigma\)-algebra or \(\sigma\)-field, which is a family of events (subsets of \(\Omega\));
  3. \(\mathbb{P}\) is a probability measure, which assigns probability to each event in \(\mathcal{A}\).

To give some intuition behind this approach, David Williams says to imagine that Tyche, Goddess of Chance, chooses a point \(\omega\in\Omega\) at random according to the law \(\mathbb{P}\) such that an event \(A\in \mathcal{A}\) has a probability given by \(\mathbb{P}(A)\), where we understand probability with our own intuition. We can also choose \(\omega\in\Omega\) by using some physical experiment, as long as it is random.

With this formalism, mathematicians define random objects by using a certain measurable function or mapping that maps to a suitable space of mathematical objects. For example, a real-valued random variable is a measurable function from \(\Omega\) to the real line. To consider other random mathematical objects, we just need to define a measurable mapping from \(\Omega\) to a suitable mathematical space.

Definition

Stochastic process

Mathematically, a stochastic process is usually defined as a collection of random variables indexed by some set, often representing time. (Other interpretations exists such as a stochastic process being a random function.)

More formally, a stochastic process is defined as a collection of random variables defined on a common probability space \((\Omega,{\cal A}, \mathbb{P} )\), where \(\Omega\) is a sample space, \({\cal A}\) is a \(\sigma\)-algebra, and \(\mathbb{P}\) is a probability measure, and the random variables, indexed by some set \(T\), all take values in the same mathematical space \(S\), which must be measurable with respect to some \(\sigma\)-algebra \(\Sigma\).

Put another way, for a given probability space \(( \mathbb{P}, {\cal A}, \Omega)\) and a measurable space \((S, \Sigma)\), a stochastic process is a collection of \(S\)-valued random variables, which we can write as:

$$\{X(t):t\in T \}.$$

For each \(t\in T\), \(X(t)\) is a random variable. Historically, a point \(t\in T\) was interpreted as time, so \(X(t)\) is random variable representing a value observed at time \(t\).

Often the collection of random variables \(\{X(t):t\in T \}\) is denoted by simply a single letter such as \(X\).  There are different notations for stochastic processes. For example, a stochastic process can also be written as \(\{X(t,\omega):t\in T \}\), reflecting that is function of the two variables, \(t\in T\) and \(\omega\in \Omega\).

Index set

The set \(T\) is called the index set or parameter set of the stochastic process. Typically this set is some subset of the real line, such as the natural numbers or an interval. If the set is countable, such as the natural numbers, then it is a discrete-time stochastic process. Conversely, an interval for the index set gives a continuous-time stochastic process.

(If the index set is some two or higher dimensional Euclidean space or manifold, then typically the resulting stochastic or random process is called a random field.)

State space

The mathematical space \(S\) is called the state space of the stochastic process. The precise mathematical space can be any one of many different mathematical sets such as the integers, the real line, \(n\)-dimensional Euclidean space, the complex plane, or more abstract mathematical spaces. The different spaces reflects the different values that the stochastic process can take.

Sample function

A single outcome of a stochastic process is called a sample function, a sample path, or, a realization. It is formed by taking a single value of each random variable of the stochastic process. More precisely, if \(\{X(t,\omega):t\in T \}\) is a stochastic process, then for any point \(\omega\in\Omega\), the mapping
\[
X(\cdot,\omega): T \rightarrow S,
\]
is a sample function of the stochastic process \(\{X(t,\omega):t\in T \}\). Other names exist such as trajectory, and path function.

Examples

The range of stochastic processes is limitless, as stochastic processes can be used to construct new ones. Broadly speaking, stochastic processes can be classified by their index set and their state space. For example, we can consider a discrete-time and continuous-time stochastic processes.

There are some commonly used stochastic processes. I’ll give the details of a couple of very simple ones.

Bernoulli process

A very simple stochastic process is the Bernoulli process, which is a sequence of independent and identically distributed (iid) random variables. The value of each random variable can be one of two values, typically \(0\) and \(1\), but they could be also \(-1\) and \(+1\) or \(H\) and \(T\). To generate this stochastic process, each random variable takes one value,  say, \(1\) with probability \(p\) or the other value, say, \(0\) with probability \(1-p\).

We can can liken this stochastic process to flipping a coin, where the probability of a head is \(p\) and its value is \(1\), while the value of a tail is \(0\). In other words, a Bernoulli process is a sequence of iid Bernoulli random variables. The Bernoulli process has the counting numbers (that is, the positive integers) as its index set, meaning \(T=1,\dots\), while in this example the state space is simply \(S=\{0,1\}\).

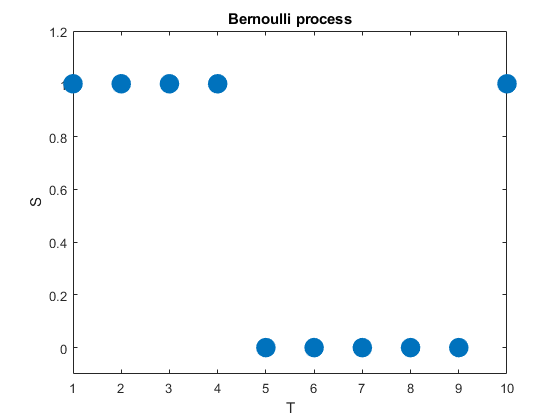
A single realization of a Bernoulli process, one of the simplest stochastic processes. This discrete-time stochastic process only takes two values such as 0 and 1.

(We can easily generalize the Bernoulli process by having a sequence of iid variables with the same probability space.)

Random walks

A random walk is a type of stochastic process that is usually defined as sum of a sequence of iid random variables or random vectors in Euclidean space. Given random walks are formed from a sum, they are stochastic processes that evolve in discrete time. (But some also use the term to refer to stochastic processes that change in continuous time.)

A classic example of this stochastic process is the simple random walk, which is based on a Bernoulli process, where each iid Bernoulli variable takes either the value positive one or negative one. More specifically, the simple random walk increases by one with probability, say, \(p\), or decreases by one with probability \(1-p\). The index set of this stochastic process is the natural numbers, while its state space is the integers.

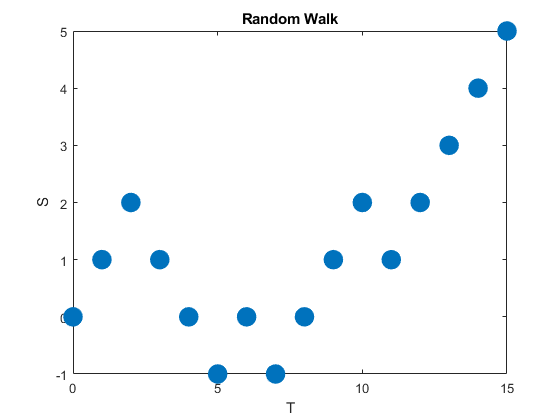
A single realization of a simple (symmetric) random walk. This discrete-time stochastic process is a fundamental object in the history of probability theory.

Random walks can be defined in more general settings such as \(n\)- dimensional Euclidean space. There are other types of random walks, defined on different mathematical objects, such as lattices and groups, and in general they are highly studied and have many applications in different disciplines.

Markov processes

One important way for classifying stochastic processes is the stochastic dependence between random variables. For the Bernoulli process, there was no dependence between any random variable, giving a very simple stochastic process. But this is not a very interesting stochastic process.

A more interesting (and typically useful) stochastic process is one in which the random variables depend on each other in some way. For example, the next position of a random walk depends on the current position, which in turn depends on the previous position.

A large family of stochastic processes in which the next value depends on the current value are called Markov processes or Markov chains. (Both names are used. The term Markov chain is largely used when either the state space or index is discrete, but there does not seem to be an agreed upon convention. When I think Markov chain, I think discrete time.) The definition of a Markov process has a property that constrains the dependence between the random variables, as the next random variable only depends on the current random variable, and not all the previous random variables. This constraint on the dependence typically renders Markov processes more tractable than general stochastic processes.

It would be difficult to overstate the importance of Markov processes. Their study and application appear throughout probability, science, and technology.

Counting processes

A counting process is a stochastic process that takes the values of non-negative integers, meaning its state space is the counting numbers, and is non-decreasing. A simple example of a counting process is an asymmetric random walk, which increases by one with some probability \(p\) or remains the same value with probability \(1-p\). In other words, the accumulative sum of a Bernoulli process.  This is an example of a discrete-time counting process, but continuous-time ones also exist.

A counting process can be also interpreted as a counting as a random counting measure on the index set.

Two important stochastic processes

The most two important stochastic processes are the Poisson process and the Wiener process (often called Brownian motion process or just Brownian motion). They are important for both applications and theoretical reasons, playing fundamental roles in the theory of stochastic processes. In future posts I’ll cover both the Wiener process and the Poisson process.

Code

The code used to create the plots in this post is found here on my code repository. The code exists in both MATLAB and Python.

Further reading

There are many, many books covering the fundamentals of modern probability theory, including those (in roughly increasing order of difficulty) by Grimmett and Stirzaker, Karr, Rosenthal, Shiryaev, Durrett, and Billingsley. A very quick introduction is given in this web article.

The development of stochastic processes is one of the great achievements in modern mathematics. Researchers and practitioners have both studied them in great depth and found many applications for them. Consequently, there is no shortage of literature on stochastic processes. For example:

Finally, one of the main pioneers of stochastic processes was Joseph Doob. His seminal book was simply called Stochastic Processes.

Point processes

A non-random collection of points located on some space is called a point pattern in spatial statistics. Informally, you can interpret a point process as a collection of random points scattered over some underlying mathematical space, meaning each outcome or realization of a point process forms a point pattern. Using such intuition gets you pretty far. But if we want to be mathematically formal, we need to use precise mathematical objects.

Historically, there’s a couple main interpretations of a point process, which is also called a random point field.  But now a standard mathematical approach is used.

In this post I will cover the main definitions, terminology and some of the notation used in the theory and application of point processes. (I refer to the next post for more on the point process notation.) I won’t delve too much into the precise details, giving just an outline with references at the end.

Underlying mathematical space

We consider a point process defined on some underlying mathematical space \(\mathbb{S}\), which is sometimes called the carrier space or state space. We further assume that the space is measurable by having a Borel \(\sigma\)-algebra \(\mathcal{S}\).

In practice, the underlying space is usually the real line \(\mathbb{R}\), the plane \(\mathbb{R}^2\), or some other familiar mathematical space like a square lattice. More generally, a point process can be defined on any metric space, allowing for the notion of distance. Mathematicians study point processes in even more general settings by defining them on, for example, a locally compact second countable Hausdorff space. But such generality is typically not needed for most people and their applications.

Modern probability approach

In modern probability theory, if we want to define a random mathematical object, we start with a random experiment in the context of a probability space or triple \((\Omega,\mathcal{A},\mathbb{P})\), where:

  1. \(\Omega\) is a sample space, which is the set of all possible outcomes;
  2. \(\mathcal{A}\) is a \(\sigma\)-algebra or \(\sigma\)-field, which is a family of events (subsets of \(\Omega\));
  3. \(\mathbb{P}\) is a probability measure, which assigns probability to each event in \(\mathcal{A}\).

To gain some intuition, David Williams says to imagine that Tyche, Goddess of Chance, chooses a sample point \(\omega\in\Omega\) at random according to the law \(\mathbb{P}\) such that an event \(A\in \mathcal{A}\) has a probability given by \(\mathbb{P}(A)\), where we understand probability with our own intuition. To bring things back to Earth, we can also choose a sample point \(\omega\in\Omega\) by using some physical experiment, as long as it is truly random, such that  the probability of \(A\in \mathcal{A}\) happening is given by \(\mathbb{P}(A)\).

Now we can define random objects by using a certain measurable function or mapping that maps to a suitable space of objects. For example, a real-valued random variable is a measurable function from \(\Omega\) to the real line; a random matrix is a measurable function from \(\Omega\) to some space of matrices; and, as John Kingman quips in his classic book Poisson Processes, a random elephant is just a measurable function from \(\Omega\) to some suitable space of elephants.

But what space should we use for a point process? To answer that, we need to interpret a point process as a suitable mathematical object.

Interpretation

There are different ways to interpret a point process, which is often denoted by a single letter, for example, \(N\) or \(\Phi\). (The convention of using the Greek letter \(\Phi\) comes from German mathematicians, but some prefer not to use \(\Phi\), as it’s often used for the normal cumulative distribution function.) If the point process is defined on a space like the real like, where the points can be ordered, then additional interpretations exist, but mathematicians assume the order of the points does not matter, limiting the possible interpretations.

Random closed set

In mathematics a collection of distinct things is formalized by a mathematical object called a set. We say that a set contains elements or members, and a set never contains more than one of the same element. Sets are fundamental objects with set concepts and notation being found everywhere in mathematics.

We now define a common type of point process, which we can formalize with the concept of a set.

A point process is simple if the probability of all points of the point process being distinct is one.

In other words, for a simple point process, there is zero probability of two or more of its points being found in the same location of the underlying state space \(\mathbb{S}\), which brings us to our first interpretation.

A simple point process can be interpreted as a random closed set.

More specifically, we can interpret a simple point process as a (measurable) mapping from a sample space \(\Omega\) to the space of closed sets \(\mathbb{F}\), meaning that each realization of a simple point process is a closed set \(\phi\in \mathbb{F}\).

Point process theory has adopted the notation from set theory. For example, if we want to say some point, which we denote by \(x\), of the underlying space \(\mathbb{S}\) belongs to or is a member of a simple point process \(\Phi\), then we can simply write \(x\in \Phi\). We can also write a point process as \(\{x\}_i\) to highlight its interpretation as a random closed set of points.

The theory of random sets, which is a field of study in its own right, can be applied to simple point processes owing to this interpretation. But for non-simple point processes, we need another point process interpretation.

Random measures

Modern integration theory is based on measure theory, which revolves around the concept of a set function known as a measure. In addition to a couple of other properties, when you apply this function to a set, it gives a number, such as a integer or real number. For example, a counting measure gives you the number elements in a set, which could be a subspace \(B\), such as a region of the plane \(B \subset \mathbb{R}^2\). (The letter \(B\) is often used for sets in measure and probability theory as it’s typically assumed that the sets are Borel sets, which form a very large family of well-behaved sets in terms of measurability.) The concept of a counting measure gives us an interpretation of a point process, which has now become the standard one.

A point process can be interpreted a random counting measure.

More specifically, we define a point process as a mapping from a sample space \(\Omega\) to the space of counting measures \(\mathbb{M}\), meaning that each realization of a point process is a counting measure \(\phi\in \mathbb{M}\). Some mathematicians even say a point process is just another name for a random counting measure. The techniques of random measure theory provide alternative (and arguably main) approach to study point processes.

This standard interpretation of a point process means that point process theory borrows heavily notation from measure theory and calculus. For example, in measure theory we can write a (non-random) counting measure as \(\#\), so \(\#(B)=n\) is how we write that the set \(B\) contains \(n\) points. We can then write the the number of points of a point process \(\Phi\) located in some (Borel) set \(B\) as \(N(B) =\#( B \cap \Phi)\), where \(N(B)\) is a random variable. In this expression, the point process is denoted by \(\Phi\), while\(N(B)\) is the number of points of \(\Phi\) in \(B\), meaning \(N\) is a random counting measure .

Important concepts

In the theory point processes, like any other field of mathematics, there are various important concepts for understanding and proving various results. Without going in the details, these include shot noise, Campbell’s theorem, Laplace functional, Palm calculus, void probability, and factorial moment measures. In future posts, I’ll detail some of these concepts.

Further reading

There are many, many books covering the fundamentals of modern probability theory, including those (in roughly order of difficulty) by Grimmett and Stirzaker, Karr, Rosenthal, Shiryaev, Durrett, and Billingsley. A very quick introduction is given in this web article.

For point process theory, Wikipedia is a good start place to start, particularly the articles on point processes and point process notation, though the former is too mathematical for a Wikipedia article. The standard reference on point processes was the An Introduction to the Theory of Point Processes by Daley and Vere-Jones, which now spread across volume one and two, but I would not learn the subject with these books.

The classic text Stochastic Geometry and its Applications by Chiu, Stoyan, Kendall and Mecke covers point processes and the varying notation in Chapters 2 and 4. The similar material is covered in the previous edition by Stoyan, Kendall and Mecke. A more mathematical book that covers point processes and random sets is Stochastic and integral geometry by Schneider and Weil. Point processes are also covered in a recent readable tutorial on Palm calculus and Gibbs point processes, which will be the subject of another post.

Spatial statistics builds of point process theory, giving good texts for learning the basics of point processes. I suggest the lectures notes by Baddeley, which form Chapter 1 of these published lectures, edited by Baddeley, Bárány, Schneider, and Weil. I always recommend the book Spatial Point Patterns: Methodology and Applications with R written by spatial statistics experts Baddeley, Rubak and Turner, which covers the spatial statistics (and point process simulation) R-package spatstat. Another good book is Statistical Inference and Simulation for Spatial Point Processes by Møller and Waagepetersen, but there are many more.

In recent years, point process theory (under the guise of stochastic geometry) has been used to model wireless networks. An early treatment of the subject is the two-volume textbook Stochastic Geometry and Wireless Networks by Baccelli and Błaszczyszyn, where the first volume is on theory and the second volume is on applications. Haenggi wrote a very readable introductory book called Stochastic Geometry for Wireless networks.

For the more mathematically brave, there’s the recent book Random Measures, Theory and Applications by Kallenberg who is the authority of the subject, having written earlier books, but these have now become obsolete with this recent publication. Another mathematically challenging book is The Theory of Random Sets by Molchanov, but it has less emphasis on point processes.

A very recent book (manuscript) is Random Measures, Point Processes, and Stochastic Geometry by Baccelli, Błaszczyszyn, and Karray, which contains much material, including new results and proofs. Finally, Last and Penrose wrote a mathematical monograph Lectures on the Poisson process, which is freely available online here.