Cholera outbreaks due to public water pumps. Suburbs serviced by hospitals. Formation of crystals. Coverage regions of phone towers. We can model or approximate all these phenomena and many, many more with a geometric structure called, among other names, a Voronoi tessellation.
To form a Voronoi tessellation, consider a collection of points scattered on some space, like the plane, where it’s easier to picture things, especially when using a Euclidean metric. Now for each point in the collection, consider the surrounding region that is closer to that point than any other point in the collection. Each region forms a cell corresponding to the point. The union of all the sets covers the underlying space. That union of sets is the Voronoi tessellation.

Mathematicians have extensively studied Voronoi tessellations, particularly those based on Poisson point processes, forming a core subject in the field of stochastic geometry.
It’s also called a Dirichlet tessellation
The main other name for the Voronoi tessellation is the Dirichlet tessellation. Historically, Dirichlet beats Voronoi, but it seems wherever I look, the name Voronoi usually wins out, suggesting an example of Stigler’s law of eponymy. A notable exception is the R library spatstat that does actually call it a Dirichlet tessellation. Wikipedia calls it a Voronoi diagram. I’ve read that Descartes studied the object even earlier than Dirichlet, but Voronoi studied it in much more depth. At any rate, I will call it a Voronoi tessellation.
Everyday Voronoi tessellations
Voronoi tessellations are just not interesting mathematical objects, as they arise in everyday situations. This piece from Scientific American website explains:
Everyone uses Voronoi tessellations, even without realizing it. Individuals seeking the nearest café, urban planners determining service area for hospitals, and regional planners outlining school districts all consider Voronoi tessellations. Each café, school, or hospital is a site from which a Voronoi tessellation is generated. The cells represent ideal service areas for individual businesses, schools, or hospitals to minimize clientele transit time. Coffee drinkers, patients, or students inside a service area (that is, a cell) should live closer to their own café, hospital, or school (that is, their own cell’s site) than any other. Voronoi tessellations are ubiquitous, yet often invisible.
Delaunay triangulation
A closely related object is the Delaunay triangulation. For a given collection of points on some underlying mathematical space, a Delaunay triangulation is formed by connecting the points and creating triangles with the condition that for each point, no other point exists in the circumcircle of the corresponding triangle. (A circumcircle is a circle that passes through all three vertices of a triangle.)

The vertices of the the Delaunay triangular and Voronoi tessellation both form graphs, which turn out to be the dual graphs of each other.
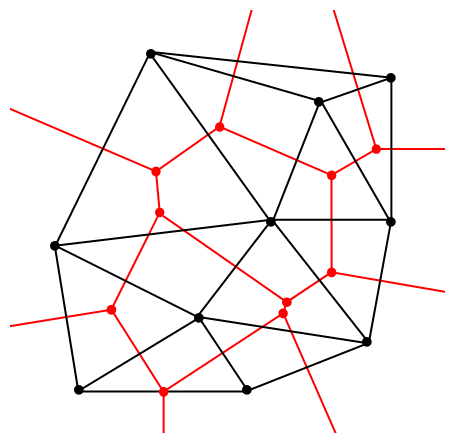
Software: Qhull
Due to its applications, it’s not surprising that there exist algorithms that quickly create or estimate Voronoi tessellations. I don’t want to implement one of these algorithms from scratch, as they have already been implemented in various scientific programming languages. Many of the languages, such as MATLAB, R, and Python (SciPy) use the code from Qhull. (Note the Qhull website calls the tessellation a Voronoi diagram.)
(The Julia programming language, which I examined in a previous post, has a Voronoi package that does not use Qhull.)
Qhull finds the Voronoi tessellation by first finding the Delaunay triangulation. If the underlying space is bounded, then all the Voronoi cells are also bounded. But on an unbounded space, it is possible to have unbounded cells, meaning their areas (or volumes) are infinite. In such cases, the algorithms sometime place virtual points at infinity, but I don’t want to focus on such details. I will assume Qhull does a good job.
Code
As always, the code from all my posts is online. For this post, the MATLAB and Python code is here and here, respectively, which generates Voronoi tesselations.
MATLAB
It is fairly straightforward to create Voronoi tessellations in MATLAB. You can just use the function voronoi, which is only for two-dimensional tessellations. (Note: the MATLAB website says the behaviour of the function voronoi has changed, so that may cause problems when using different versions of MATLAB.) The function requires two inputs as vectors, say, x and y, corresponding to the Cartesian (or \(x\) and \(y\)) coordinates of the points. If you just run the voronoi command, it will create and plot a Voronoi tessellation (or Voronoi diagram, as MATLAB calls it). But the MATLAB website also describes how to plot the tessellation manually.
For \(d\) -dimensional tessellations, there is the function voronoin, which requires a single input. The single output consists of combining \(d\) column vectors for the Cartesian coordinates. For example, given the column vectors x, y and z, then the input is [x, y, z].
If you give the functions voronoi or voronoin output arguments, then the tessellation is not plotted and instead two data structures, say, v and c are created for describing the vertices of the tessellation. I generally use voronoi for plotting, but I use voronoin (and not voronoi) for generating vertex data, so I will focus on the outputs of voronoin.
For voronoin, the first (output) data structure v is simply an two-dimensional array array that contain the Cartesian coordinates of every vertex in the Voronoi tessellation. The second (output) data structure c is a cell array describing the vertices of each Voronoi cell (it has to be a cell array, as opposed to a regular array, as the cells have varying number of vertices). Each entry of the cell array contains a one-dimensional array with array indices corresponding to the \(x\) and \(y\) coordinates.
The code checks which Voronoi cells are unbounded by seeing if they have vertices at infinity, which corresponds to a \(1\) in the index arrays (stored in the structure array c).
One criticism of the MATLAB functions is that they don’t return all the information of the Voronoi tessellation. More specifically, the functions don’t return the boundaries between the unbounded cells, though voronoi internally calculates and uses these boundaries to generate Voronoi plots. This is covered in this review on different Voronoi packages. Conversely, the Python package returns more information such as that of the edges or ridges of the Voronoi cells.
Python
To create the Voronoi tessellation, use the SciPy (Spatial) function Voronoi. This function does \(d\)-dimensional tessellations. For the two-dimensional setting, you need to input the \(x\) and \(y\) coordinates as a single array of dimensions \(2 \times n\), where \(n\) is the number of points in the collection. In my code, I start off with two one-dimensional arrays for the Cartesian coordinates, but then I combined them into a single array by using the function numpy.stack with the function argument axis =1.
I would argue that the Voronoi function in SciPy is not as intuitive to use as the MATLAB version. One thing I found a bit tricky, at first, is that the cells and the points have a different sets of numbering (that is, they are indexed differently). (And I am not the only one that was caught by this.) You must use the attribute called point_region to access a cell number (or index) from a point number (or index). In my code the attribute is accessed and then called it indexP2C, which is an integer array with cell indices. Of course, there could be a reason for this, and I am just failing to understand it.
Apart from the above criticism, the function Voronoi worked well. As I mentioned before, this package returns more Voronoi information than the MATLAB equivalents.
To plot the Voronoi tessellation, use the SciPy function voronoi_plot_2d, which allows for various plotting options, but it does require Matplotlib. The input is the data object created by the function Voronoi.
Results
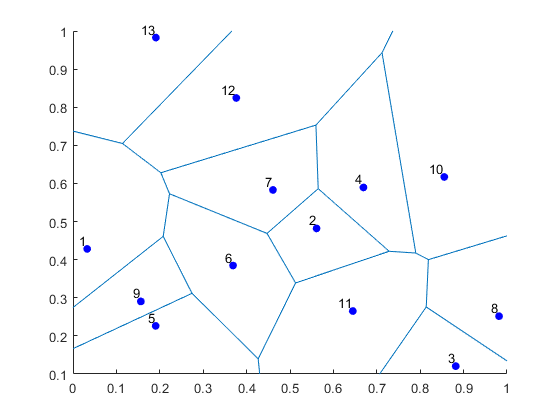
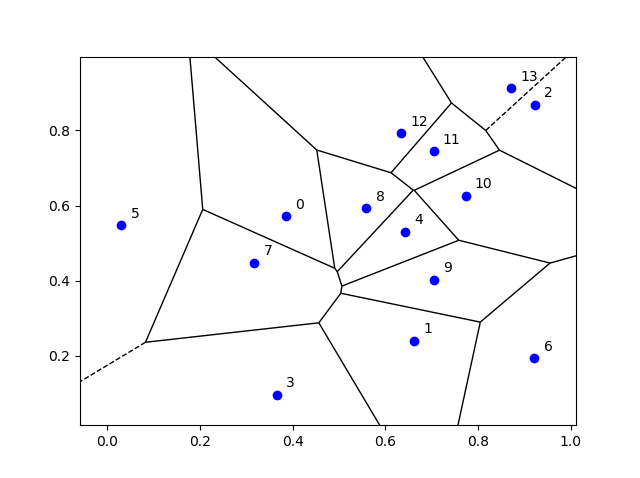
I’ve plotted the results for a single realization of a Poisson point process. I’ve also plotted the indices of the points. Recall that the indexing in Python and MATLAB start respectively at zero and one.
MATLAB
Python
Voronoi animations
I took the animation of evolving Voronoi cells, which appears in the introduction, from Wikipedia. The creator generated it in MATLAB and also posted the code online. The code is long, and I wouldn’t even dare to try to reproduce it, but I am glad someone else wrote it.
Such animations exist also for other metrics. For example, the Manhattan metric (or taxi cab or city block metric) gives the animation below, where the growing disks have been replaced with squares.

This Wikipedia user page has animations under other metrics on Euclidean space.
This post also features animations of Voronoi tessellations when the points move.
Further reading
There is a lot of literature on Voronoi or Dirichlet tessellations, particularly when the seeds of the cells form a Poisson point process. The references in the articles on Wikipedia and MathWorld are good starting points.
Here is a good post on Voronoi tesselations. Here is a non-mathematical article published in the Irish Times.
For the more mathematically inclined, there is also the monograph Lectures on random Voronoi tessellations by Møller.



Hello Paul,
I am really pleased with your explanation on voronoi diagram in matlab.Please I need help with the code for voronoi circle also showing its vertices since the vertex is the centre of each voronoi circle.I also need the code for computing the radius of each voronoi circle.
I look forward to getting a feedback from you. Thanks Paul.
Thank you for your comment, Theresa. By centre of each “Voronoi circle”, do you mean the geometric centre or centroid of each Voronoi cell? MATLAB has a function called centroid that calculates that. I use the centroid function here:
https://github.com/hpaulkeeler/voronoi_uniform
More specifically, see the file VoronoiUniformTest.m, where I use the centroid function in the for-loop (starting around line 98) to test that the simulated/sampled points are statistically uniform. See this post for more details.
By radius, I suppose you mean the largest distance from the centre a vertex? You should be able to calculate that when you have the centroid. All the best.
Thank you for the great Article. I wonder if there is an established method to obtain tessellation maps for a cluster of triangular shapes. Suppose we have “n” triangles all with the same size and shape and we randomly throw them in a rectangular box. How can we obtain a tessellation map that does not cut any of the triangles?
I am not really a computational geometry person. So I don’t know the answer to your question. I am actually having trouble to understand it. For a Voronoi tessellation, you need “seeds” for the cells. Are the triangles your seeds? And the triangles overlap.
I probably won’t be able to help you. But it is a computational geometry question.
https://en.wikipedia.org/wiki/Computational_geometry
Hello,
If we have a known square and some points inside that square, then we can have voronoi diagram. Now my question is, can we get the voronoi vertices only inside the square? Also I want the points of intersection of the voronoi diagram with the sqaure. Can we get that?
Hi Subjajit,
Thanks for your message. Your question has two parts.
1) When a Voronoi function does the calculations, typically it doesn’t know that your points are located inside a square or not. You just give the function the points, but no information about the square (or bounding box), so the points could be located in a square or any shape larger than the square. What to do?
The pre-written Voronoi functions in MATLAB, Python etc (which often use qhull) will give you vertices outside the square. These functions assume there’s a vertex at infinity. You can see that if you look at this example on the MATLAB website:
https://www.mathworks.com/help/matlab/ref/voronoin.html
Note the 10×2 vector v contains a point at infinity.
2) To find the points where the Voronoi diagram intersects with the square (or bounding box) is a bit tricky. If you’re doing it in MATLAB, I would start here:
https://blogs.mathworks.com/loren/2011/08/29/intersecting-lines/
https://blogs.mathworks.com/loren/2011/09/08/intersecting-lines-part-2/
I think I know how to solve this problem, but I need some time to write a blog post about it.
i need voronoi tesselation for cuboid (i.e., dividing cuboid into random shaped….) as like dividing Fe block as random shaped fe grains.
how to do it in matlab, i mean how can i visualise in matlab for 3d voronoi?
MATLAB has a couple Voronoi functions. I would check out the last example:
https://mathworks.com/help/matlab/math/voronoi-diagrams.html
There’s also this function:
https://mathworks.com/help/matlab/ref/voronoin.html
You should be able to use this also:
https://mathworks.com/help/matlab/ref/plot3.html
I modified that code to go through and plot only the finite Voronoi cells. This should get you started, if I understand your request correctly.
close all; clearvars; clc;6rng('default');
X = -3 + 6.*rand([25 3]);
dt = delaunayTriangulation(X);
[V,R] = voronoiDiagram(dt);
numbCells=length(R);
figure;
hold on;
%loop through all the cells and plot only the finite ones
for indexCell=1:numbCells
XR10 = V(R{indexCell},:);
%check for points at infinity (ie index one)
boolePlot=~any(R{indexCell}==1);
if boolePlot
K = convhull(XR10);
defaultFaceColor = rand(1,3);
trisurf(K, XR10(:,1) ,XR10(:,2) ,XR10(:,3) , ...
'FaceColor', defaultFaceColor, 'FaceAlpha',0.8)
end
end
title('3-D Voronoi Region');