Deep learning refers several classes of statistical models, most often neural networks, which are deep in the sense that they have many layers between the input and output. We can think of these layers as computational stages.
(More precisely, you can think of them as very big matrices.)
These statistical models have now become interchangeable with the much loved term artificial intelligence (AI). But how do neural networks work?
Neural networks are collections of large — often extraordinarily large — matrices with values that have been carefully chosen (or found) so that running inputs through these matrices generates accurate outputs for certain problems like classifying photos or writing readable sentences. There are many types of neural networks, but to understand them, it’s best to start with a basic one, which is an approach I covered in a previous post.
Without using any of the neural network libraries in MATLAB or Python (of which there are several), I wrote a simple four-layer feedforward (neural) network, which is also called a multilayer perceptron. This is an unadorned neural network without any of the fancy bells and whistles that they now possess.
And that’s all you need to understand the general gist of deep learning.
Binary classification problem
I applied the simple neural network to the classic problem of binary classification. More specifically, I created a simple problem by divided two-dimensional (Cartesian) square into two non-overlapping regions. My neural network needs to identify in region a point lies in a square. A simple problem, but it is both fundamental and challenging.
I created three such problems with increasing difficulty. Here they are:
- Simple: Ten points of two types located in a square, where the classification border between the two types is curve lined.
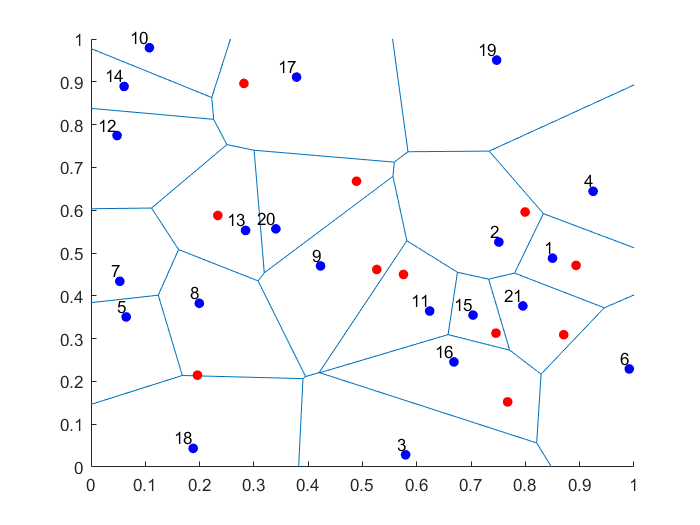
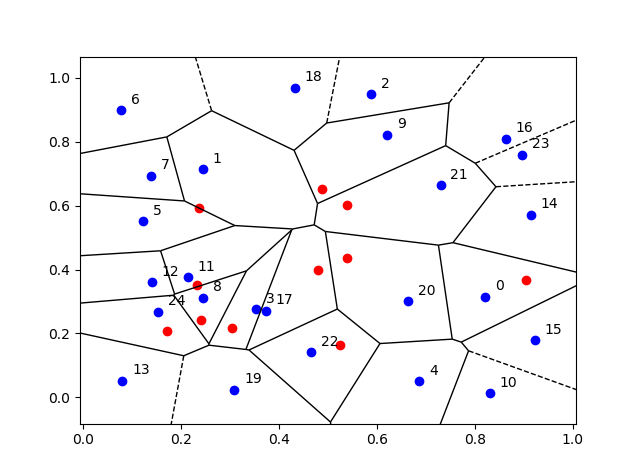
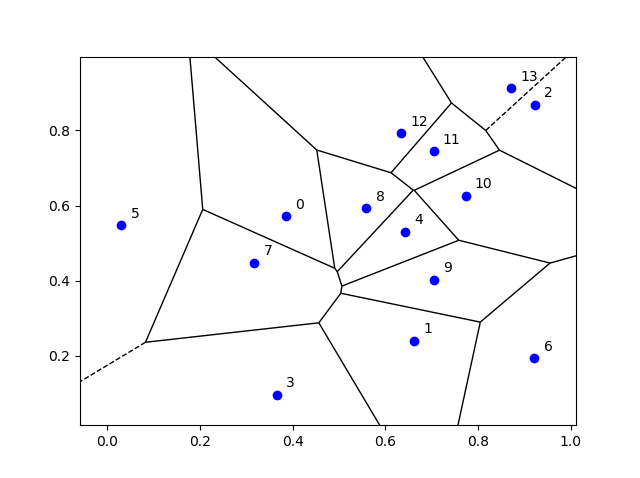
- Voronoi: A Voronoi tessellation is (deterministically) created with a small number of seeds (or Voronoi cells). A point can either be in a given Voronoi cell or not, hence there are two types of points.
- Rose: A simple diagram of a four-petal flower or rose is created using a polar coordinates. Located entirely inside a square, points can either be inside the rose or not, giving two types of points.
Components of the neural network model
Optimization method
I fitted or or trained my four-layer neural network model by using a simple stochastic gradient descent method. The field of optimization (or operations research) abounds with methods based on gradients (or derivatives), which usually fall under the category of convex optimziation.
In the code I wrote, a random coordinate is chosen, and then the fitting (or optimization) method takes a step where the gradient is the largest, where the size of step is dictated by a fixed constant called a learning rate. This procedure is repeated for some pre-fixed number of steps. The random choosing of the coordinate is done with replacement.
This is basically the simplest training method you can use. In practice, you never use such simple methods, relying upon more complex gradient-based methods such as Adam.
Cost function
For training, the so-called cost function or loss function is a root-mean-square function, which goes against the flow today, as most neural networks now employ cost functions based on the maximum likelihood and cross-entropy. There is a good reason why these are used instead of the root-mean-square. They work much better.
Activation function
For the activation function, the code uses the sigmoid function, but you can easily change it to use recitified linear unit (ReLU), which is what most neural networks use today. For decades, it commonly accepted to use the sigmoid function, partly because it’s smooth. But it seems only work well for small networks. The rectified linear unit reigns supreme now, as it is considerably better than the sigmoid function and others in large neural networks.
Code
I stress that this code is only for educational purposes. It’s designed to gain intuition into how (simple) neural networks do what they do.
If you have a problem that requires neural networks (or deep learning), then use one of the libraries such as PyTorch or TensorFlow. Do not use my code for such problems.
I generally found that the MATLAB code run much faster and smoother than the Python code. Python isn’t great for speed. (Serious libraries are not written in Python but C or, like much of the matrix libraries in Python, Fortran.)
Here’s my code.
MATLAB
% This code runs a simple feedforward neural network inspired.
%
% The neural network is a multi-layer perceptron designed for a simple
% binary classification. The classification is determining whether a
% two-dimensional (Cartesian) point is located inside some given region or
% not.
%
% For the simple binary examples used here, the code seems to work for
% sufficiently large number of optimization steps, typically in the 10s and
% 100s of thousands.
%
% This neural network only has 4 layers (so 2 hidden layers). The
% trainning procedure, meaning the forward and backward passes, are
% hard-coded. This means changing the number of layers requires additional
% information on the neural network architecture.
%
% It uses the sigmoid function; see the activate function.
%
% NOTE: This code is for illustration and educational purposes only. Use a
% industry-level library for real problems.
%
% Author: H. Paul Keeler, 2019.
% Website: hpaulkeeler.com
% Repository: github.com/hpaulkeeler/posts
clearvars; clc; close all;
choiceData=3; %choose 1, 2 or 3
numbSteps = 2e5; %number of steps for the (gradient) optimization method
rateLearn = 0.05; %hyperparameter
numbTest = 1000; %number of points for testing the fitted model
boolePlot=true;
rng(42); %set seed for reproducibility of results
%generating or retrieving the training data
switch choiceData
case 1
%%% simple example
%recommended minimum number of optimization steps: numbSteps = 1e5
x1 = 2*[0.1,0.3,0.1,0.6,0.4,0.6,0.5,0.9,0.4,0.7]-1;
x2 = 2*[0.1,0.4,0.5,0.9,0.2,0.3,0.6,0.2,0.4,0.6]-1;
numbTrainAll = 10; %number of training data
%output (binary) data
y = [ones(1,5) zeros(1,5); zeros(1,5) ones(1,5)];
case 2
%%% voronoi example
%recommended minimum number of optimization steps: numbSteps = 1e5
numbTrainAll = 1000; %number of training data
x1 = 2*rand(1,numbTrainAll)-1;
x2=2*rand(1,numbTrainAll)-1;
booleInsideVoroni=checkVoronoiInside(x1,x2);
% output (binary) data
y=[booleInsideVoroni;~booleInsideVoroni];
case 3
%%% rose/flower example
%recommended minimum number of optimization steps: numbSteps = 2e5
numbTrainAll=1000; %number of training data
x1=2*rand(1,numbTrainAll)-1;
x2=2*rand(1,numbTrainAll)-1;
booleInsideFlower=checkFlowerInside(x1,x2);
%output (binary) data
y=[booleInsideFlower;~booleInsideFlower];
end
x=[x1;x2];
booleTrain = logical(y);
%dimensions/widths of neural network
numbWidth1 = 2; %must be 2 for 2-D input data
numbWidth2 = 4;
numbWidth3 = 4;
numbWidth4 = 2; %must be 2 for binary output
numbWidthAll=[numbWidth1,numbWidth2,numbWidth3,numbWidth4];
numbLayer=length(numbWidthAll);
%initialize weights and biases
scaleModel = .5;
W2 = scaleModel * randn(numbWidth2,numbWidth1);
b2 = scaleModel * rand(numbWidth2,1);
W3 = scaleModel * randn(numbWidth3,numbWidth2);
b3 = scaleModel * rand(numbWidth3,1);
W4 = scaleModel * randn(numbWidth4,numbWidth3);
b4 = scaleModel * rand(numbWidth4,1);
%create arrays of matrices
%w matrices
arrayW{1}=W2;
arrayW{2}=W3;
arrayW{3}=W4;
%b vectors
array_b{1}=b2;
array_b{2}=b3;
array_b{3}=b4;
%activation matrices
arrayA=mat2cell(zeros(sum(numbWidthAll),1),numbWidthAll);
%delta (gradient) vectors
array_delta=mat2cell(zeros(sum(numbWidthAll(2:end)),1),numbWidthAll(2:end));
costHistory = zeros(numbSteps,1); %record the cost for each step
for i = 1:numbSteps
%forward and back propagation
indexTrain=randi(numbTrainAll);
xTrain = x(:,indexTrain);
%run forward pass
A2 = activate(xTrain,W2,b2);
A3 = activate(A2,W3,b3);
A4 = activate(A3,W4,b4);
%new (replaces above three lines)
arrayA{1}=xTrain;
for j=2:numbLayer
arrayA{j}=activate(arrayA{j-1},arrayW{j-1},array_b{j-1});
end
%run backward pass (to calculate the gradient) using Hadamard products
delta4 = A4.*(1-A4).*(A4-y(:,indexTrain));
delta3 = A3.*(1-A3).*(transpose(W4)*delta4);
delta2 = A2.*(1-A2).*(transpose(W3)*delta3);
%new (replaces above three lines)
A_temp=arrayA{numbLayer};
array_delta{numbLayer-1}=A_temp.*(1-A_temp).*(A_temp-y(:,indexTrain));
for j=numbLayer-1:-1:2
A_temp=arrayA{j};
delta_temp=array_delta{j};
W_temp=arrayW{j};
array_delta{j-1}= A_temp.*(1-A_temp).*(transpose(W_temp)*delta_temp);
end
%update using steepest descent
%transpose of xTrains used for W matrices
W2 = W2 - rateLearn*delta2*transpose(xTrain);
W3 = W3 - rateLearn*delta3*transpose(A2);
W4 = W4 - rateLearn*delta4*transpose(A3);
b2 = b2 - rateLearn*delta2;
b3 = b3 - rateLearn*delta3;
b4 = b4 - rateLearn*delta4;
%new (replaces above six lines)
for j=1:numbLayer-1
A_temp=arrayA{j};
delta_temp=array_delta{j};
arrayW{j}=arrayW{j} - rateLearn*delta_temp*transpose(A_temp);
array_b{j}=array_b{j} - rateLearn*delta_temp;
end
%update cost
costCurrent_i = getCost(x,y,arrayW,array_b,numbLayer);
costHistory(i) = costCurrent_i;
end
%generating test data
xTest1 = 2*rand(1,numbTest)-1;
xTest2 = 2*rand(1,numbTest)-1;
xTest = [xTest1;xTest2];
booleTest = (false(2,numbTest));
%testing every point
for k=1:numbTest
xTestSingle = xTest(:,k);
%apply fitted model
yTestSingle = feedForward(xTestSingle,arrayW,array_b,numbLayer);
[~,indexTest] = max(yTestSingle);
booleTest(1,k) = (indexTest==1);
booleTest(2,k) = (indexTest==2);
end
if boolePlot
%plot history of cost
figure;
semilogy(1:numbSteps,costHistory);
xlabel('Number of optimization steps');
ylabel('Value of cost function');
title('History of the cost function')
%plot training data
figure;
tiledlayout(1,2);
nexttile;
hold on;
plot(x1(booleTrain(1,:)),x2(booleTrain(1,:)),'rs');
plot(x1(booleTrain(2,:)),x2(booleTrain(2,:)),'b+');
xlabel('x');
ylabel('y');
title('Training data');
axis([-1,1,-1,1]);
axis square;
%plot test data
nexttile;
hold on;
plot(xTest1(booleTest(1,:)),xTest2(booleTest(1,:)),'rd');
plot(xTest1(booleTest(2,:)),xTest2(booleTest(2,:)),'bx');
xlabel('x');
ylabel('y');
title('Testing data');
axis([-1,1,-1,1]);
axis square;
end
function costTotal = getCost(x,y,arrayW,array_b,numbLayer)
numbTrainAll = max(size(x));
%originally y, x1 and x2 were defined outside this function
costAll = zeros(numbTrainAll,1);
for i = 1:numbTrainAll
%loop through every training point
x_i = x(:,i);
A_Last=feedForward(x_i,arrayW,array_b,numbLayer);
%find difference between algorithm output and training data
costAll(i) = norm(y(:,i) - A_Last,2);
end
costTotal = norm(costAll,2)^2;
end
function y = activate(x,W,b)
z=(W*x+b);
%evaluate sigmoid (ie logistic) function
y = 1./(1+exp(-z));
%evaluate ReLU (rectified linear unit)
%y = max(0,z);
end
function A_Last= feedForward(xSingle,arrayW,array_b,numbLayer)
%run forward pass
A_now=xSingle;
for j=2:numbLayer
A_next=activate(A_now,arrayW{j-1},array_b{j-1});
A_now=A_next;
end
A_Last=A_next;
end
function booleFlowerInside=checkFlowerInside(x1,x2)
% This function creates a simple binary classification problem.
% A single point (x1,x2) is either inside a flower petal or not, where the
% flower (or rose) is defined in polar coordinates by the equation:
%
% rho(theta) =cos(k*theta)), where k is a positive integer.
orderFlower = 2;
[thetaFlower, rhoFlower] = cart2pol(x1(:)',x2(:)');
% check if point (x1,x2) is inside the rose
booleFlowerInside = abs(cos(orderFlower*thetaFlower)) <= rhoFlower;
end
function booleVoronoiInside=checkVoronoiInside(x1,x2)
% This function creates a simple binary classification problem.
% A single point (x1,x2) is either inside a chosen Voronoi cell or not,
% where the Voronoi cells are defined deterministically below.
numbPoints = length(x1);
% generat some deterministic seeds for the Voronoi cells
numbSeed = 6;
indexCellChosen = 4; %arbitrary chosen cells from first up to this number
t = 1:numbSeed;
% a deterministic points located on the square [-1,+1]x[-1,+1]
xSeed1 = sin(27*t.*pi.*cos(t.^2*pi+.4)+1.4);
xSeed2 = sin(4.7*t.*pi.*sin(t.^3*pi+.7)+.3);
xSeed = [xSeed1;xSeed2];
% find which Voroinoi cells each point (x1,x2) belongs to
indexVoronoi = zeros(1,numbPoints);
for i = 1:numbPoints
x_i = [x1(i);x2(i)]; %retrieve single point
diff_x = xSeed-x_i;
distSquared_x = diff_x(1,:).^2+diff_x(2,:).^2; %relative distance squared
[~,indexVoronoiTemp] = min(distSquared_x); %find closest seed
indexVoronoi(i) = indexVoronoiTemp;
end
% see if points are inside the Voronoi cell number indexCellSingle
booleVoronoiInside = (indexVoronoi==indexCellChosen);
end
Python
The use of matrices in Python are kindly described as an afterthought. So it takes a bit of Python sleight of hand to get MATLAB code translated into working Python code.
(This stems partly from the fact that Python is row-major, as the language it’s built upon, C, whereas MATLAB is column-major, as its inspiration, Fortran.)
# This code runs a simple feedforward neural network.
#
# The neural network is a multi-layer perceptron designed for a simple
# binary classification. The classification is determining whether a
# two-dimensional (Cartesian) point is located inside some given region or
# not.
#
# For the simple binary examples used here, the code seems to work for
# sufficiently large number of optimization steps, typically in the 10s and
# 100s of thousands.
#
# This neural network only has 4 layers (so 2 hidden layers). The
# trainning procedure, meaning the forward and backward passes, are
# hard-coded. This means changing the number of layers requires additional
# information on the neural network architecture.
#
# It uses the sigmoid function; see the activate function.
#
# NOTE: This code is for illustration and educational purposes only. Use a
# industry-level library for real problems.
#
# For more details, see the post:
#
# https://hpaulkeeler.com/creating-a-simple-feedforward-neural-network-without-libraries/
#
# Author: H. Paul Keeler, 2019.
# Website: hpaulkeeler.com
# Repository: github.com/hpaulkeeler/posts
import numpy as np; # NumPy package for arrays, random number generation, etc
import matplotlib.pyplot as plt # For plotting
#from FunctionsExamples import checkFlowerInside, checkVoronoiInside
plt.close('all'); # close all figures
choiceData=1; #choose 1, 2 or 3
numbSteps = 1e5; #number of steps for the (gradient) optimization method
rateLearn = 0.05; #hyperparameter
numbTest = 1000; #number of points for testing the fitted model
boolePlot = True;
np.random.seed(42); #set seed for reproducibility of results
#helper functions for generating problems
def checkFlowerInside(x1,x2):
# This function creates a simple binary classification problem.
# A single point (x1,x2) is either inside a flower petal or not, where the
# flower (or rose) is defined in polar coordinates by the equation:
#
# rho(theta) =cos(k*theta)), where k is a positive integer.
orderFlower = 2;
thetaFlower = np.arctan2(x2,x1);
rhoFlower = np.sqrt(x1**2+x2**2);
# check if point (x1,x2) is inside the rose
booleFlowerInside = np.abs(np.cos(orderFlower*thetaFlower)) <= rhoFlower;
return booleFlowerInside
def checkVoronoiInside(x1,x2):
# This function creates a simple binary classification problem.
# A single point (x1,x2) is either inside a chosen Voronoi cell or not,
# where the Voronoi cells are defined deterministically below.
numbPoints = len(x1);
# generat some deterministic seeds for the Voronoi cells
numbSeed = 6;
indexCellChosen = 4; #arbitrary chosen cells from first up to this number
t = np.arange(numbSeed)+1;
# a deterministic points located on the square [-1,+1]x[-1,+1]
xSeed1 = np.sin(27*t*np.pi*np.cos(t**2*np.pi+.4)+1.4);
xSeed2 = np.sin(4.7*t*np.pi*np.sin(t**3*np.pi+.7)+.3);
xSeed = np.stack((xSeed1,xSeed2),axis=0);
# find which Voroinoi cells each point (x1,x2) belongs to
indexVoronoi = np.zeros(numbPoints);
for i in range(numbPoints):
x_i = np.stack((x1[i],x2[i]),axis=0).reshape(-1, 1); #retrieve single point
diff_x = xSeed-x_i;
distSquared_x = diff_x[0,:]**2+diff_x[1,:]**2; #relative distance squared
indexVoronoiTemp = np.argmin(distSquared_x); #find closest seed
indexVoronoi[i] = indexVoronoiTemp;
# see if points are inside the Voronoi cell number indexCellSingle
booleVoronoiInside = (indexVoronoi==indexCellChosen);
return booleVoronoiInside
#generating or retrieving the training data
if (choiceData==1):
### simple example
#recommended minimum number of optimization steps: numbSteps = 1e5
x1 = 2*np.array([0.1,0.3,0.1,0.6,0.4,0.6,0.5,0.9,0.4,0.7])-1;
x2 = 2*np.array([0.1,0.4,0.5,0.9,0.2,0.3,0.6,0.2,0.4,0.6])-1;
numbTrainAll = 10; #number of training data
#output (binary) data
y = np.array([[1,1,1,1,1,0,0,0,0,0],[0,0,0,0,0,1,1,1,1,1]]);
x=np.stack((x1,x2),axis=0);
if (choiceData==2):
### voronoi example
#recommended minimum number of optimization steps: numbSteps = 1e5
numbTrainAll = 500; #number of training data
x=2*np.random.uniform(0, 1,(2,numbTrainAll))-1;
x1 = x[0,:];
x2 = x[1,:];
booleInsideVoroni=checkVoronoiInside(x1,x2);
# output (binary) data
y=np.stack((booleInsideVoroni,~booleInsideVoroni),axis=0);
if (choiceData==3):
### rose/flower example
#recommended minimum number of optimization steps: numbSteps = 2e5
numbTrainAll=100; #number of training data
x=2*np.random.uniform(0, 1,(2,numbTrainAll))-1;
x1 = x[0,:];
x2 = x[1,:];
booleInsideFlower=checkFlowerInside(x1,x2);
#output (binary) data
y=np.stack((booleInsideFlower,~booleInsideFlower),axis=0);
#helper functions for training and running the neural network
def activate(x,W,b):
z=np.matmul(W,x)+b;
#evaluate sigmoid (ie logistic) function
y = 1/(1+np.exp(-z));
#evaluate ReLU (rectified linear unit)
#y = np.max(0,z);
return y
def feedForward(xSingle,arrayW,array_b,numbLayer):
#run forward pass
A_now=xSingle;
for j in np.arange(1,numbLayer):
A_next=activate(A_now,arrayW[j-1],array_b[j-1]);
A_now=A_next;
A_Last=A_next;
return A_Last;
def getCost(x,y,arrayW,array_b,numbLayer):
numbTrainAll = np.max(x.shape);
#originally y, x1 and x2 were defined outside this function
costAll = np.zeros((numbTrainAll,1));
for i in range(numbTrainAll):
#loop through every training point
x_i = x[:,i].reshape(-1, 1);
A_Last=feedForward(x_i,arrayW,array_b,numbLayer);
#find difference between algorithm output and training data
costAll[i] = np.linalg.norm(y[:,i].reshape(-1, 1) - A_Last,2);
costTotal = np.linalg.norm(costAll,2)**2;
return costTotal
#dimensions/widths of neural network
numbWidth1 = 2; #must be 2 for 2-D input data
numbWidth2 = 4;
numbWidth3 = 4;
numbWidth4 = 2; #must be 2 for binary output
numbWidthAll=np.array([numbWidth1,numbWidth2,numbWidth3,numbWidth4]);
numbLayer=len(numbWidthAll);
#initialize weights and biases
scaleModel = .5;
W2 = scaleModel * np.random.normal(0, 1,(numbWidth2,numbWidth1));
b2 = scaleModel * np.random.uniform(0, 1,(numbWidth2,1));
W3 = scaleModel * np.random.normal(0, 1,(numbWidth3,numbWidth2));
b3 = scaleModel * np.random.uniform(0, 1,(numbWidth3,1));
W4 = scaleModel * np.random.normal(0, 1,(numbWidth4,numbWidth3));
b4 = scaleModel * np.random.uniform(0, 1,(numbWidth4,1));
#create lists of matrices
#w matrices
arrayW=[];
arrayW.append(W2);
arrayW.append(W3);
arrayW.append(W4);
#b vectors
array_b=[];
array_b.append(b2);
array_b.append(b3);
array_b.append(b4);
#activation matrices
arrayA=[];
for j in range(numbLayer):
arrayA.append(np.zeros(numbWidthAll[j]).reshape(-1, 1).T);
#delta (gradient) vectors
array_delta=[];
for j in range(numbLayer-1):
array_delta.append(np.zeros(numbWidthAll[j+1]).reshape(-1, 1).T);
numbSteps=int(numbSteps)
costHistory = np.zeros((numbSteps,1));
booleTrain = y;
for i in range(numbSteps):
#forward and back propagation
indexTrain=np.random.randint(numbTrainAll);
xTrain = x[:,indexTrain].reshape(-1, 1);
#run forward pass
arrayA[0]=xTrain; #treat input as the A1 matrix
for j in (range(numbLayer-1)):
arrayA[j+1]=activate(arrayA[j],arrayW[j],array_b[j]);
#run backward pass (to calculate the gradient) using Hadamard products
A_temp=arrayA[-1];
array_delta[-1]=A_temp*(1-A_temp)*(A_temp-y[:,indexTrain].reshape(-1, 1));
for j in np.arange(numbLayer-2,0,-1):
A_temp=arrayA[j];
delta_temp=array_delta[j];
W_temp=arrayW[j];
array_delta[j-1]= A_temp*(1-A_temp)*np.matmul(np.transpose(W_temp),delta_temp);
#update using steepest descent
#transpose of xTrains used for W matrices
for j in range(numbLayer-1):
A_temp=arrayA[j];
delta_temp=array_delta[j];
arrayW[j]=arrayW[j] - rateLearn*np.matmul(delta_temp,np.transpose(A_temp));
array_b[j]=array_b[j] - rateLearn*delta_temp;
#update cost
costCurrent_i = getCost(x,y,arrayW,array_b,numbLayer);
costHistory[i] = costCurrent_i;
#generating test data
xTest = 2*np.random.uniform(0,1,(2,numbTest))-1;
xTest1 = xTest[0,:];
xTest2 = xTest[1,:];
booleTest = np.zeros((2,numbTest));
#testing every point
for k in range(numbTest):
xTestSingle = xTest[:,k].reshape(-1, 1);
#apply fitted model
yTestSingle = feedForward(xTestSingle,arrayW,array_b,numbLayer);
indexTest = np.argmax(yTestSingle, axis=0);
booleTest[0,k] = ((indexTest==0)[0]);
booleTest[1,k] = ((indexTest==1)[0]);
if boolePlot:
#plot history of cost
plt.figure();
plt.semilogy(np.arange(numbSteps)+1,costHistory);
plt.xlabel('Number of optimization steps');
plt.ylabel('Value of cost function');
plt.title('History of the cost function')
#plot training data
fig, ax = plt.subplots(1, 2);
ax[0].plot(x1[np.where(booleTrain[0,:])],x2[np.where(booleTrain[0,:])],\
'rs', markerfacecolor='none');
ax[0].plot(x1[np.where(booleTrain[1,:])],x2[np.where(booleTrain[1,:])],\
'b+');
ax[0].set_xlabel('x');
ax[0].set_ylabel('y');
ax[0].set_title('Training data');
ax[0].set_xlim([-1, 1])
ax[0].set_ylim([-1, 1])
ax[0].axis('equal');
#plot test data
ax[1].plot(xTest1[np.where(booleTest[0,:])],xTest2[np.where(booleTest[0,:])],\
'rd', markerfacecolor='none');
ax[1].plot(xTest1[np.where(booleTest[1,:])],xTest2[np.where(booleTest[1,:])],\
'bx');
ax[1].set_xlabel('x');
ax[1].set_ylabel('y');
ax[1].set_title('Testing data');
ax[1].set_xlim([-1, 1])
ax[1].set_ylim([-1, 1])
ax[1].axis('equal');
Results
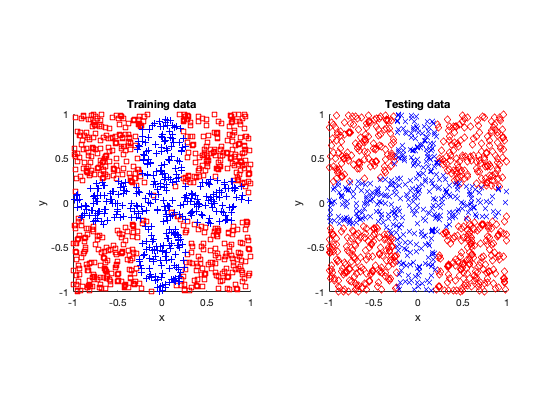
After fitting or training the models, I tested them by applying the fitted neural network to other data. (In machine learning and statistics, you famously don’t use the same data to train and test a model.)
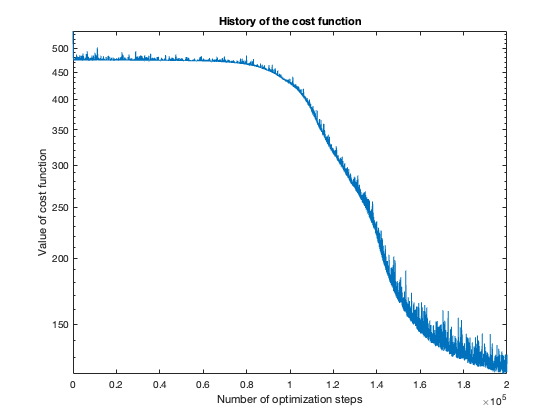
The number of steps needed to obtain reasonable results was about 100 thousand. To get a feeling of this, look at the plot of the cost function value over the number of optimization steps. For more complicated problems, such as the flower or rose problem, even more steps were needed.
I found the Python code, which is basically a close literal translation (by me) of the MATLAB code, too slow, so I generated the results using MATLAB.
Note: These results were generated with stochastic methods (namely, the training method), so my results will not agree exactly with yours, but hopefully they’ll be close enough.
Simple
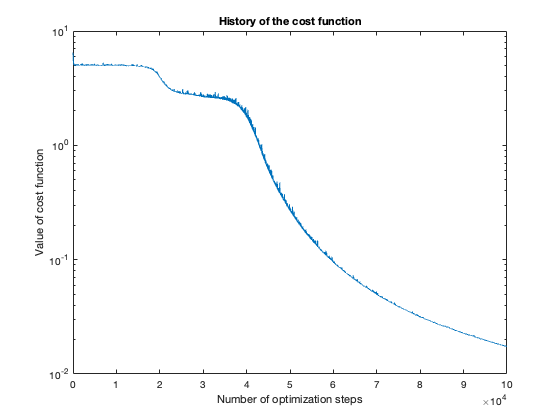

Voronoi
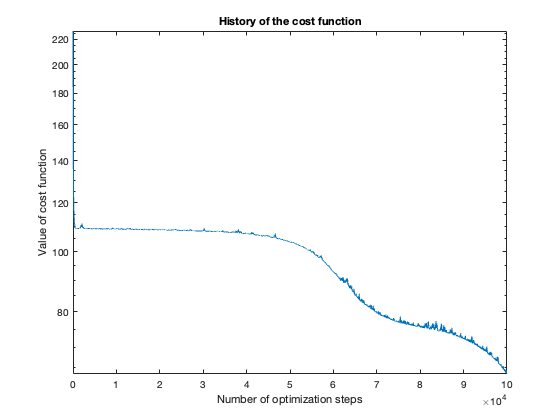
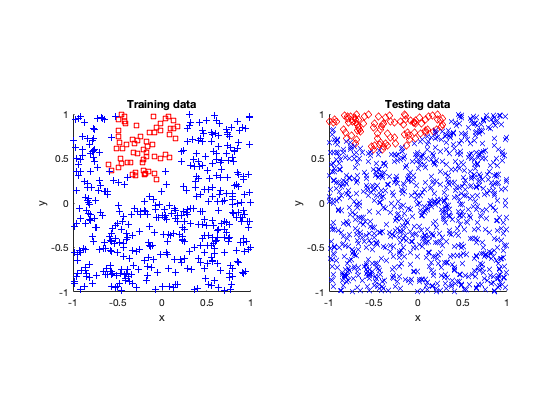
Rose
The rose problem was the most difficult to classify. Sometimes it was a complete fail. Sometimes the training method could only see one component of the rose. It worked a couple of times, namely with 20 thousand optimization steps and a random seed of 42.
I imagine this problem is difficult due to the obvious complex geometry. Specifically, the both ends of each petal become thin, which is where the testing breaks down.
Fail
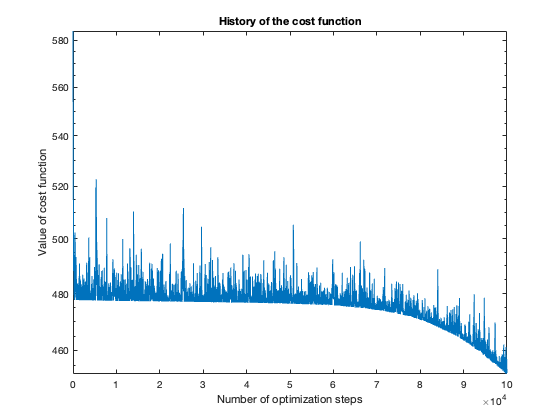
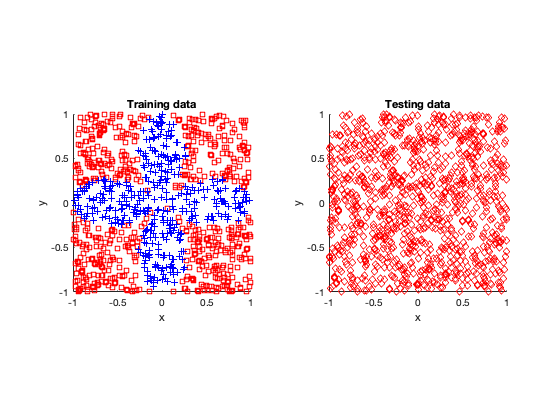
Half-success
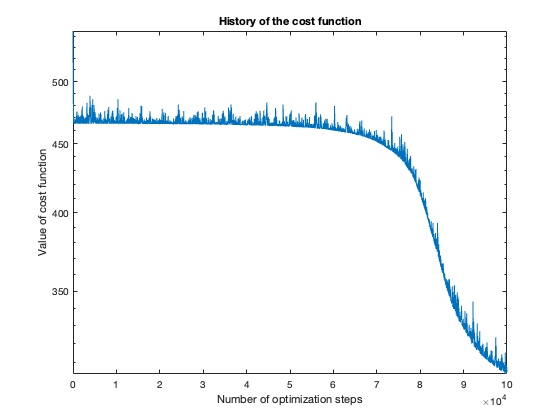
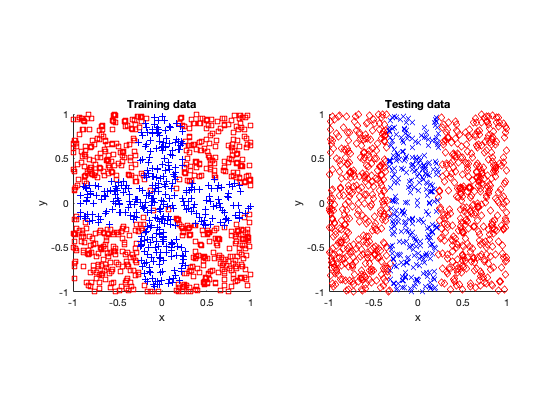
Success (mostly)
Further reading
There is just so many things to read on neural networks, particularly on the web. This post was inspired by this tutorial paper:
- 2019 – Higham and Higham, Deep Learning: An Introduction for Applied Mathematicians.
I covered this paper in a previous post.
For a readable book, I recommend this book:
- Goodfellow, Bengio, Courville – Deep Learning – MIT Press.